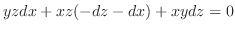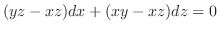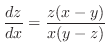Next: 6.9 陰関数 Up: 確認問題詳解 Previous: 6.7 2変数関数の極値 索引
(a)
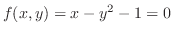 とおき,全微分を求めると,
とおき,全微分を求めると,
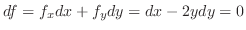 .これより,
.これより,
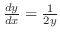 .
次に,
.
次に,
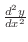 を求める.
を求める.
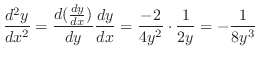
(b)
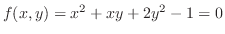 とおき,全微分を求めると,
とおき,全微分を求めると,
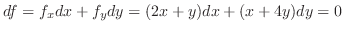 .これより,
.これより,
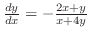 .
次に,
.
次に,
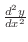 を求める.
を求める.
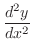 |
 |
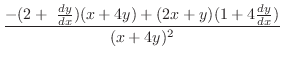 |
|
 |
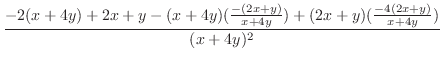 |
||
 |
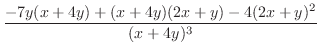 |
||
 |
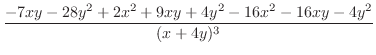 |
||
 |
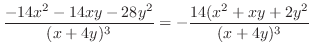 |
(c)
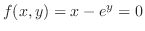 とおき,全微分を求めると,
とおき,全微分を求めると,
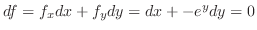 .これより,
.これより,
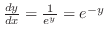 .
次に,
.
次に,
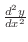 を求める.
を求める.
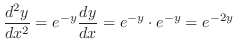
(d)
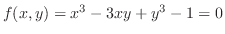 とおき,全微分を求めると,
とおき,全微分を求めると,
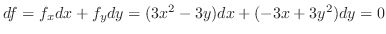 .これより,
.これより,
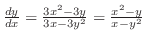 .
次に,
.
次に,
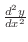 を求める.
を求める.
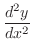 |
 |
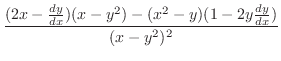 |
|
 |
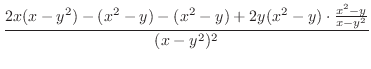 |
||
 |
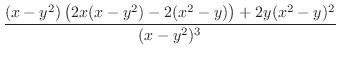 |
||
 |
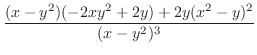 |
||
 |
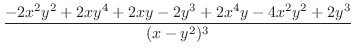 |
||
 |
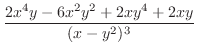 |
||
 |
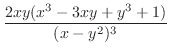 |
2.
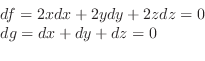
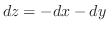 で置き換えると,
で置き換えると,
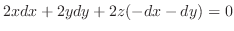
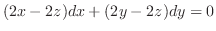
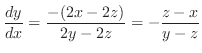
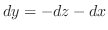 で置き換えると,
で置き換えると,
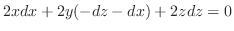
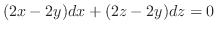
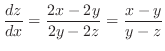
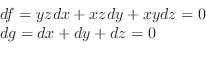
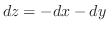 で置き換えると,
で置き換えると,
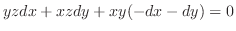
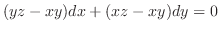
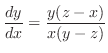
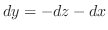 で置き換えると,
で置き換えると,