Next: 6.8 陰関数 Up: 確認問題詳解 Previous: 6.6 合成関数の偏微分法 索引
1.
2変数関数のTaylorの定理
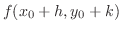 |
 |
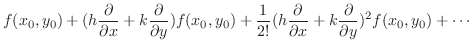 |
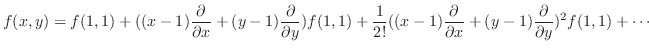
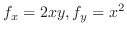
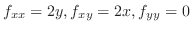
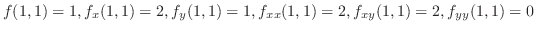
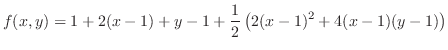 |
|||
 |
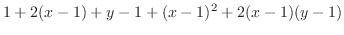 |
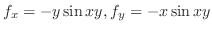
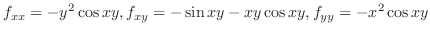
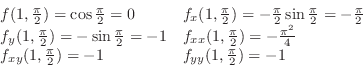
したがって,
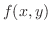 |
 |
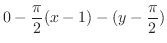 |
|
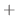 |
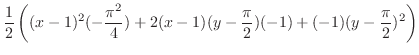 |
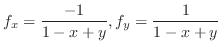
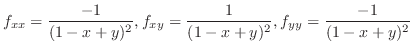
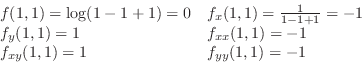
したがって,
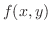 |
 |
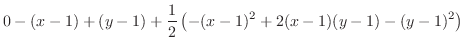 |
|
 |
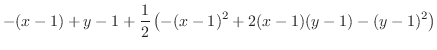 |
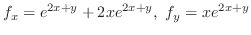
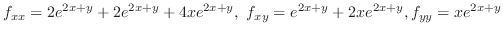
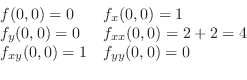
したがって,
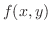 |
 |
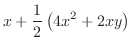 |
2.
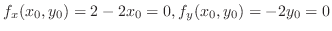
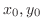 について解くと
について解くと
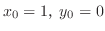 .
次に
.
次に
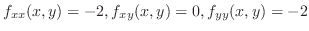 ,
,
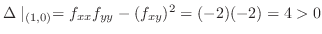 より
より
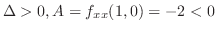 となるので
となるので
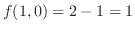 は極大値.
は極大値.
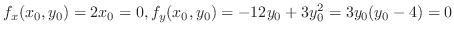
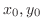 について解くと
について解くと
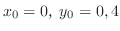 .
次に
.
次に
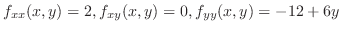 ,
,
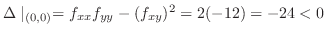 より
より 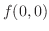 は鞍点.また,
は鞍点.また,
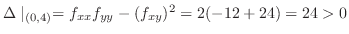 ,
,
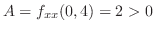 より
より
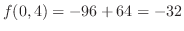 は極小値.
は極小値.
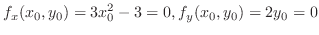
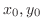 について解くと
について解くと
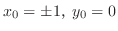 .
次に
.
次に
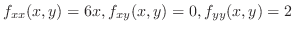 ,
,
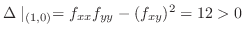 より
より
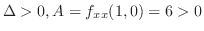 となるので,
となるので,
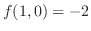 は極小値.また,
は極小値.また,
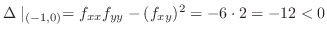 より
より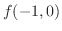 は鞍点
は鞍点
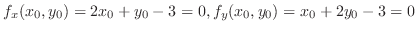
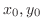 について解くと
について解くと
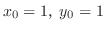 .
次に
.
次に
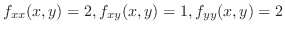 ,
,
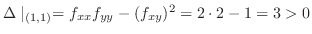 より
より
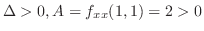 となるので,
となるので,
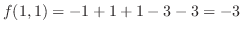 は極小値.
は極小値.