Next: 関数の極限(limit of function) Up: 関数(FUNCTIONS) Previous: 関数の定義(definition of function) 目次 索引
これから微分積分学を学んでいく上で必要な関数をまとめておきます.
変数  と定数との間に,加法,減法,乗法の3つの演算を有限回行なって得られる関数を 整関数(polynomial) といいます.つまり,
と定数との間に,加法,減法,乗法の3つの演算を有限回行なって得られる関数を 整関数(polynomial) といいます.つまり,

変数  と定数との間に,加法,減法,乗法,除法の4つの演算を有限回行なって得られる関数を 有理関数(rational function) といいます.つまり,
と定数との間に,加法,減法,乗法,除法の4つの演算を有限回行なって得られる関数を 有理関数(rational function) といいます.つまり,
 整式
整式
変数  と定数との間に,加減乗除の4つの演算のほかに,さらに開法(n乗根を求める演算)を有限回行なって得られる関数を 無理関数(irrational function) といいます.つまり
と定数との間に,加減乗除の4つの演算のほかに,さらに開法(n乗根を求める演算)を有限回行なって得られる関数を 無理関数(irrational function) といいます.つまり
![$\displaystyle \sqrt[n]{Q(x)}, \ Q(x)$](img376.png) 有理関数
有理関数
直角を90度とする表わし方を度数法といいますが,90という数字に大切な意味があるのでしょうか.別に直角は100度でもよかったのではないでしょうか.実際,度数法は数学を勉強していくうえで,十分ではありません.そこで,ここでは弧度法とよばれる角の測り方について,考えてみます.図1.2のように,原点をOとし,単位円
 の周上に点
の周上に点
 をとり,
をとり,
 を
を 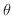 とおきます.点Pが単位円周上を一周したときの円周の長さは
とおきます.点Pが単位円周上を一周したときの円周の長さは  .またそのときの角
.またそのときの角 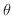 を度数法で表わすと360度となります.同様に,単位円周上を
を度数法で表わすと360度となります.同様に,単位円周上を
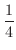 動けば,そのときの弧の長さは
動けば,そのときの弧の長さは
 ,角
,角 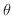 は 90度となることが分かります.この考え方をもう少し広げて,弧APの長さが1となるときの角
は 90度となることが分かります.この考え方をもう少し広げて,弧APの長さが1となるときの角
 を1弧度(radian)と表わしたのが 弧度法(radian) とよばれるものです.これより,次のような関係式が生まれます.
を1弧度(radian)と表わしたのが 弧度法(radian) とよばれるものです.これより,次のような関係式が生まれます.
 が度数法で
が度数法で  , 弧度法で
, 弧度法で 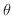 のとき,
のとき,

これより,主要な角を度数法と弧度法で表わすと次のようになります.
| 度数 | 0 | 30 | 45 | 60 | 90 | 120 | 150 | 180 | 360 |
| 弧度 | 0 |
 |
 |
 |
 |
 |
 |
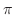 |
 |
弧度法を用いると点Pの座標を角
 の関数と考えて次のような関数を定義することができます.これらをまとめて三角関数とよびます.
の関数と考えて次のような関数を定義することができます.これらをまとめて三角関数とよびます.


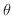 の代わりに
の代わりに を変数とした形で与えられます.つまり
を変数とした形で与えられます.つまり


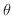 に対して,
に対して,

解 図1.2で動径OPの長さは1より

 . したがって,
. したがって,

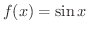 のグラフを描いてみましょう.
のグラフを描いてみましょう.
解
図1.2において
 となることが分かります.したがって,
となることが分かります.したがって,
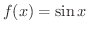 は奇関数です.演習問題1-1-6bで,奇関数の特徴は原点対称なグラフであることを学びました.そこで,
は奇関数です.演習問題1-1-6bで,奇関数の特徴は原点対称なグラフであることを学びました.そこで,
 のグラフを描くには,
のグラフを描くには, の値が0〜
の値が0〜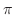 までのときの
までのときの の値を調べればよいことが分かります.図1.2より,
の値を調べればよいことが分かります.図1.2より,
 のとき
のとき
 .
.
 のとき
のとき
 .このように
.このように 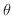 の値を変えながら
の値を変えながら  の値を調べると,
の値を調べると,


解
 より
より
 .
これを満たす範囲を図示すると,
.
これを満たす範囲を図示すると,
 を満たす
を満たす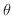 は
は


 のグラフを描いてみましょう.
のグラフを描いてみましょう.
解
図1.2において
 となることが分かります.したがって,
となることが分かります.したがって,
 は偶関数です.演習問題1-1-6bで,偶関数の特徴は
は偶関数です.演習問題1-1-6bで,偶関数の特徴は 軸対称なグラフであることを学びました.そこで,
軸対称なグラフであることを学びました.そこで,
 のグラフを描くには,
のグラフを描くには, の値が0〜
の値が0〜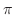 までのときの
までのときの の値を調べればよいことが分かります. 図1.2において
の値を調べればよいことが分かります. 図1.2において
 のとき
のとき
 .
.
 のとき
のとき
 .このように
.このように 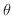 の値を変えながら
の値を変えながら  の値を調べると,
の値を調べると,


解
 より
より
 . これを満たす範囲を図示すると,
. これを満たす範囲を図示すると,
 を満たす
を満たす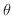 は
は


 のグラフを描いてみましょう.
のグラフを描いてみましょう.
解 図1.2において

 は奇関数です.演習問題1-1-6bで,奇関数の特徴は原点対称なグラフであることを学びました.また,
は奇関数です.演習問題1-1-6bで,奇関数の特徴は原点対称なグラフであることを学びました.また,

 は
は
 で,定義されていません.そこで,
で,定義されていません.そこで,
 のグラフを描くには,
のグラフを描くには, の値が0〜
の値が0〜
 までのときの
までのときの の値を調べればよいことが分かります.
図1.2において
の値を調べればよいことが分かります.
図1.2において
 のとき
のとき
 .
.
 のとき
のとき
 .このように
.このように 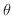 の値を変えながら
の値を変えながら  の値を調べると,
の値を調べると,


解
 を満たす範囲を図示すると,
を満たす範囲を図示すると,
 を満たす
を満たす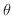 は
は


逆三角関数(inverse trigonometric function)
閉区間
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img439.png) を定義域としたとき,
を定義域としたとき,
 は1対1の関数になるので,逆関数を考えることができます.この関数を
は1対1の関数になるので,逆関数を考えることができます.この関数を
 または
または
 の値域
の値域 ![$[-1,1]$](img442.png) となり,値域は
となり,値域は
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img439.png) となります.つまり
となります.つまり

 の値域を 逆正弦関数の主値(principle value of arc sine) といいます.なぜなら
の値域を 逆正弦関数の主値(principle value of arc sine) といいます.なぜなら
 となる
となる  の値は区間
の値は区間
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img439.png) 以外にも沢山あるのに,区間
以外にも沢山あるのに,区間
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img439.png) から
から  を選ぶと決めたからです.
を選ぶと決めたからです.
 はどうやったら求まるのでしょうか.
はどうやったら求まるのでしょうか.
解
まず
 とは
とは
 のことなのですが,このとき
のことなのですが,このとき  の値は
の値は
![$\displaystyle{[\frac{-\pi}{2}, \frac{\pi}{2}]}$](img449.png) の中に入っていなければなりません.そこで
の中に入っていなければなりません.そこで
![$\displaystyle{[\frac{-\pi}{2}, \frac{\pi}{2}]}$](img449.png) の中から
の中から
 となる
となる  を捜すと,
を捜すと,
 を得るでしょう.この値が
を得るでしょう.この値が
 となります.
となります.

閉区間 ![$[0,\pi]$](img451.png) を定義域としたとき,
を定義域としたとき,
 は1対1の関数になるので,逆関数を考えることができます.この関数を
は1対1の関数になるので,逆関数を考えることができます.この関数を

 の値域
の値域 ![$[-1,1]$](img442.png) となり,値域は
となり,値域は ![$[0,\pi]$](img451.png) となります.つまり
となります.つまり

 の値域を 逆余弦関数の主値(principle value of arc cosine) といいます.
の値域を 逆余弦関数の主値(principle value of arc cosine) といいます.
開区間
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img439.png) を定義域としたとき,
を定義域としたとき,
 は1対1の関数になるので,逆関数を考えることができます.この関数を
は1対1の関数になるので,逆関数を考えることができます.この関数を

 の値域
の値域
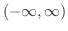 となり,値域は
となり,値域は
 となります.つまり
となります.つまり

 の値域を 逆正椄関数の主値(principle value of arc tangent) といいます.
の値域を 逆正椄関数の主値(principle value of arc tangent) といいます.
 軸とのなす角を求めよう.ただし,
軸とのなす角を求めよう.ただし,
 .
.
 とします.
とします.
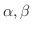 に対して,次の公式が成り立つことを示そう.
に対して,次の公式が成り立つことを示そう.
(a)
 (加法定理)
(加法定理)
(b)
 (複号同順)
(複号同順)
(c)
 (半角の公式)
(半角の公式)
(d)
 (積から和への公式)
(積から和への公式)
(e)
 (和から積への公式)
(和から積への公式)
 において,
において,
 が成り立つことを示そう.
が成り立つことを示そう.
ここで取り上げた関数のほかにも,初等関数とよばれるものに,ベキ関数,指数関数,対数関数,双曲線関数があります.ではなぜこれらを今取り上げないのかといいますと理由があるのです.ちょっとその理由を説明しましょう.例として,ベキ関数を考えます.
 をベキ関数といいます.ここで
をベキ関数といいます.ここで 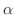 は実数です.
は実数です.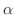 が整数のときは,
が整数のときは,  を
を 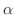 回かけるということになり問題ありません.
回かけるということになり問題ありません.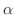 が有理数
が有理数
 のときは,
のときは,  を
を  回かけたものの
回かけたものの  乗根をとるということになり問題ありません.しかし,
乗根をとるということになり問題ありません.しかし, 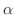 が無理数のときはどうでしょう.例えば,
が無理数のときはどうでしょう.例えば,
 のときを考えて下さい.
のときを考えて下さい.
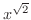 をどう考えたらよいのでしょう.
をどう考えたらよいのでしょう. を
を 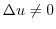 回かけることはできません.なぜなら
回かけることはできません.なぜなら 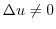 は
は
 と終なく続く数です.ではどう考えればよいのでしょう.実は,いろいろな考え方があるのですが,どれも実数の連続性とよばれる公理を基にしています.つまり,
と終なく続く数です.ではどう考えればよいのでしょう.実は,いろいろな考え方があるのですが,どれも実数の連続性とよばれる公理を基にしています.つまり, 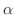 が無理数のときは,有理数のときと違いもう少し体系的に考えていかなくてはならないのです.そこで,いますぐ取り上げず,皆さんが微積分学を理解するのに必要な道具がそろったところで,自然な形であらわれるようにしたいのです.
が無理数のときは,有理数のときと違いもう少し体系的に考えていかなくてはならないのです.そこで,いますぐ取り上げず,皆さんが微積分学を理解するのに必要な道具がそろったところで,自然な形であらわれるようにしたいのです.