Next: 初等関数(elementary functions) Up: 関数(FUNCTIONS) Previous: 関数(FUNCTIONS) 目次 索引
2つの集合の間の関係を決める規則を関数といいます.ここでは,実数の集合を考えます.
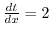 を実数全体の集合とします.
を実数全体の集合とします.
ある実数の集合 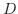 に属する各数
に属する各数  に対して,実数
に対して,実数  が1つ定まるような規則
が1つ定まるような規則  を
を 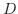 から
から
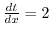 への 1価関数(single-valued function),または単に関数といいます.また,各数
への 1価関数(single-valued function),または単に関数といいます.また,各数  に対して,実数
に対して,実数  が2つ以上定まるような規則を 多価関数(multi-valued function) といい, 共に
が2つ以上定まるような規則を 多価関数(multi-valued function) といい, 共に
 で表わし,
で表わし,  は
は  の関数であるといい,
の関数であるといい, 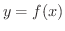 で表わします.このとき,
で表わします.このとき,  を独立変数,
を独立変数,  を従属変数といいます.
を従属変数といいます.
 の各数
の各数  に対して,実数
に対して,実数  が
が  の 2乗を 4倍したものと,
の 2乗を 4倍したものと,  の 3乗を -3倍したものの和となるように定めた規則
の 3乗を -3倍したものの和となるように定めた規則  は 1価関数でしょうか.また,
は 1価関数でしょうか.また,  を求めてみましょう.
を求めてみましょう.
解
各数  に対して,
に対して,
 という実数
という実数  が1つ定まるので
が1つ定まるので  は1価関数です.また,
は1価関数です.また,
 となります.
となります.

このように変数  と定数との間に足し算,引き算,掛け算という3つの演算を用いて得られた関数
と定数との間に足し算,引き算,掛け算という3つの演算を用いて得られた関数
 を整式といいます.また,
を整式といいます.また,  を
を  の2乗の6倍と
の2乗の6倍と  を3倍したものの和で割って得られる関数
を3倍したものの和で割って得られる関数

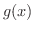 の平方根をとって得られる関数
の平方根をとって得られる関数

上の関数の定義にでてきた 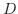 を関数
を関数  の 定義域(domain) といい
の 定義域(domain) といい  で表わします.つまり,
で表わします.つまり,  は
は  が実数となるような実数
が実数となるような実数  の集合のことです.そこで,これを
の集合のことです.そこで,これを

と表わします.ここで,  とは,
とは,  は
は  の元である.つまり
の元である.つまり  は実数であることを意味しています.
は実数であることを意味しています.
また,  を
を  の 像(image) といい,その集合を 値域(range) といい
の 像(image) といい,その集合を 値域(range) といい  で表わします.つまり,
で表わします.つまり,

これら  と
と  を
を 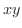 平面上に点として描いていくと,関数
平面上に点として描いていくと,関数  のグラフとよばれるものができます.つまり,集合
のグラフとよばれるものができます.つまり,集合
 が関数
が関数  の グラフ(graph) で,
の グラフ(graph) で,  で表わします.
で表わします.
 の定義域を求めてみましょう.
の定義域を求めてみましょう.
解

 が実数になるには分母が
が実数になるには分母が
 であることに注意すると,
であることに注意すると,
 より
より

 の定義域と値域を求め,
の定義域と値域を求め,  のグラフを描いてみましょう.
のグラフを描いてみましょう.
解
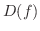 |
 |
 |
|
 |
![$\displaystyle (-\infty, -1] \cup [1,\infty)$](img276.png) |


さて,関数 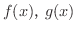 の作られ方をみていると,
の作られ方をみていると,  と
と 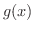 の間に四則の演算を定義することができるでしょう.
の間に四則の演算を定義することができるでしょう.
 のとき,
のとき,




解 区分的に定義された関数の和,差,積を求めるには,2つの関数の区分を同じにする必要があります.つまり,

 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |

1.1 で関数どうしの四則の演算について学びました.ここでは関数どうしのつなぎ方として,合成法則(composition) とよばれる方法について考えます.
まず,  と
と 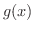 2つの関数を用意します.次に任意の
2つの関数を用意します.次に任意の  に対して規則
に対して規則 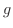 を用いて1つの実数
を用いて1つの実数 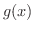 を取り出します.もしこの
を取り出します.もしこの 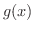 が関数
が関数  の定義域に入っていれば,規則
の定義域に入っていれば,規則  を用いて1つの実数
を用いて1つの実数  を取り出すことができるでしょう.ところで,この実数
を取り出すことができるでしょう.ところで,この実数  は何なのでしょうか.
は何なのでしょうか.
もし 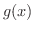 の値域が
の値域が  の定義域に含まれていれば,
の定義域に含まれていれば, 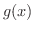 の定義域内の各数
の定義域内の各数  に対して,
に対して,  を作ることができます.これは
を作ることができます.これは 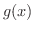 の定義域内の各数
の定義域内の各数  に対し,ただ1つの実数
に対し,ただ1つの実数  を定める規則と考えられます.よってこの規則を
を定める規則と考えられます.よってこの規則を  と
と 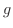 の 合成関数(composite function) といい,
の 合成関数(composite function) といい,  で表わすと
で表わすと
 となります.
となります.
 ,
,
 のとき
のとき
 を求めてみましょう.
を求めてみましょう.
解

 を求めると
を求めると


このように,合成の順序を変えると答が違ってくることがあります.これは実生活の中でも経験します.例えば, 円の商品を
円の商品を 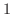 割増しにしたものを
割増しにしたものを  円引で売るのと,
円引で売るのと, 円引にしてから
円引にしてから 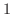 割増しにするので値段が違うことと同じ関係です.
割増しにするので値段が違うことと同じ関係です.
逆関数(inverse functions)
関数  の定義域
の定義域  内の任意の2数
内の任意の2数
 に対して,
に対して,

 は 1対1の関数(one-to-one function) であるといいます.ここで
は 1対1の関数(one-to-one function) であるといいます.ここで
 とは,
とは, 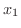 と
と 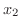 が異なるならば,
が異なるならば,  と
と  は異なることを意味しています.この場合,値域
は異なることを意味しています.この場合,値域
 の各数
の各数  に対して,
に対して, 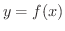 であるような
であるような  を1つ定めるような規則が考えられます(なぜでしょうか).これを
を1つ定めるような規則が考えられます(なぜでしょうか).これを  の 逆関数(inverse function) とよび,
の 逆関数(inverse function) とよび,  には逆関数が存在するといいます.また,
には逆関数が存在するといいます.また,  の逆関数を
の逆関数を  で表わします.
で表わします. の定義域は
の定義域は
 で値域は
で値域は  です.つまり,
です.つまり,

 の独立変数は
の独立変数は  で,従属変数は
で,従属変数は  ですが,独立変数を表わすときは
ですが,独立変数を表わすときは  を使うのになれているので,
を使うのになれているので,  と
と  を入れ替えて
を入れ替えて
 と表わすことがよくあります.つまり,
と表わすことがよくあります.つまり,


となります.
 は 1対1の関数か調べてみましょう.
は 1対1の関数か調べてみましょう.
解 1対1であるためには


 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
![$\displaystyle (x_{1} - x_{2})[(x_{1} + \frac{x_{2}}{2})^2 + \frac{3x_{2}^2}{4}] = 0$](img325.png) |
||
 |
 |
 は1対1の関数であることが示せました.
は1対1の関数であることが示せました.

関数のグラフが描ける場合, 軸と平行に線を引いて,2点以上グラフと交わるとこの関数は1対1ではありません.
軸と平行に線を引いて,2点以上グラフと交わるとこの関数は1対1ではありません.
もう少しして,微分について学ぶと関数  が1対1か調べるのに便利な方法があります.
関数
が1対1か調べるのに便利な方法があります.
関数  の定義域
の定義域  に含まれる任意の2数
に含まれる任意の2数
 に対して,
に対して,

 において,関数
において,関数  は 狭義の単調増加関数(strictly increasing function) であるといい,
は 狭義の単調増加関数(strictly increasing function) であるといい,

 において,関数
において,関数  は 狭義の単調減少関数(strictly decreasing function) であるといいます.
これらをあわせて狭義の単調関数といいます.この定義から明らかなように(なぜなら
は 狭義の単調減少関数(strictly decreasing function) であるといいます.
これらをあわせて狭義の単調関数といいます.この定義から明らかなように(なぜなら  と
と  はいつも異なる),狭義の単調関数は1対1になります.よって次の定理を得ます.
はいつも異なる),狭義の単調関数は1対1になります.よって次の定理を得ます.
 に対して,関数
に対して,関数  が存在し,すべての
が存在し,すべての
 に対し
に対し


 を求めてみましょう.
を求めてみましょう.
解
まず,この関数が1対1の関数であることを示します.
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
 を用います.
を用います.

 について解くと
について解くと
 .よって
.よって
 となります.
となります.

 の値が1のとき
の値が1のとき の値を求めよう.
の値を求めよう.
 および
および
 のグラフをもとに次の関数のグラフの概形を描こう.
のグラフをもとに次の関数のグラフの概形を描こう.
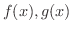 について,
について,
 と
と  を求めよう.
を求めよう.
 は,
は,
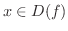 で,
で,
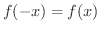 を満たすとき偶関数(even function)であるといい,
を満たすとき偶関数(even function)であるといい,
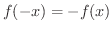 を満たすとき奇関数(odd function)であるといいます.次の関数は偶関数か奇関数か調べよう.
を満たすとき奇関数(odd function)であるといいます.次の関数は偶関数か奇関数か調べよう.
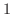 価関数か多価関数か調べよう.
価関数か多価関数か調べよう.
 のグラフを描こう.
のグラフを描こう.
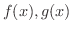 について,
について,
 と
と  を求めよう.
を求めよう.
(a) 偶関数と偶関数の積と偶関数と奇関数の積はどうなるか.
(b) 偶関数の特徴と奇関数の特徴について述べよう.