Next: 面積分(surface integrals) Up: ベクトル解析(VECTOR ANALYSIS) Previous: ベクトル場の発散(divergence of vector field) 目次 索引
2点 R,Q を結ぶ曲線  が与えられているとします. ただし,この曲線は滑らかな曲線とします.
が与えられているとします. ただし,この曲線は滑らかな曲線とします. に沿って測った弧長を
に沿って測った弧長を 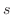 とします.すると5章で学んだように曲線上の点
とします.すると5章で学んだように曲線上の点
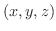 は弧長
は弧長 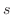 をパラメターとして表わすことができます.よって曲線
をパラメターとして表わすことができます.よって曲線  の方程式は
の方程式は

 にはそれぞれ点 R,Q が対応しているとします.このとき曲線
にはそれぞれ点 R,Q が対応しているとします.このとき曲線
 上の任意の点P
上の任意の点P 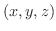 に対して定義されたスカラー場を
に対して定義されたスカラー場を
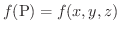 とします.
とします.
曲線  を
を  個の弧
個の弧
 に分割し,この分割を
に分割し,この分割を 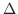 で表わします.各曲線
で表わします.各曲線  の弧長を
の弧長を
 とし,
とし,  の中に任意の点
の中に任意の点
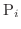 をとり次の和を考えます.
をとり次の和を考えます.

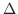 を限りなく小さくしたとき
を限りなく小さくしたとき  が極限値
が極限値  に近づくならば,この極限値
に近づくならば,この極限値  をスカラー場
をスカラー場  の
の  に沿っての 線積分(line integral) といい,
に沿っての 線積分(line integral) といい,

で表わします.曲線  が閉じているときは
が閉じているときは

線積分の定義は,今までの積分と同じRiemann和によるものなので,線積分においても次の公式が成り立つのは明らかです.

また,曲線  が滑らかではないが有限個の滑らかな曲線
が滑らかではないが有限個の滑らかな曲線
 をつなげてできているとき,この曲線を 区分的に滑らかな曲線(piecewise smooth curve) といい,このような曲線に沿っての線積分は
をつなげてできているとき,この曲線を 区分的に滑らかな曲線(piecewise smooth curve) といい,このような曲線に沿っての線積分は

 を線積分してみましょう.ただし,
を線積分してみましょう.ただし,  は点
は点  と
と  を結ぶ直線とします.
を結ぶ直線とします.
解
点  と点
と点  を結ぶ直線をパラメター表示すると
を結ぶ直線をパラメター表示すると

 は
は
 で表わされ,曲線
で表わされ,曲線  の弧長
の弧長 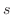 は
は

 となり,求める線積分は
となり,求める線積分は

次に向きのついた曲線
 と
と  の上で定義されたベクトル場
の上で定義されたベクトル場
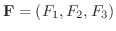 が与えられているとします.ここで
が与えられているとします.ここで  の接線単位ベクトル
の接線単位ベクトル
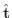 を曲線
を曲線  の正の方向(長さが増加する方向)での接線単位ベクトルとします.すると
の正の方向(長さが増加する方向)での接線単位ベクトルとします.すると
 は
は  上で定義されたスカラー場となるので,このスカラー場の曲線
上で定義されたスカラー場となるので,このスカラー場の曲線  に沿っての線積分は
に沿っての線積分は

 の向きのついた曲線
の向きのついた曲線  に沿っての線積分といいます.特に
に沿っての線積分といいます.特に


で表わすことができます.
ここでベクトル場Fが電場の場合を考えると,
 は正の電荷が点Pから点Sまで曲線
は正の電荷が点Pから点Sまで曲線  にそって移動するとき,電場Fが行なう単位電荷あたりの仕事と考えることができ,これを2点間の電位差または電圧といいます.
にそって移動するとき,電場Fが行なう単位電荷あたりの仕事と考えることができ,これを2点間の電位差または電圧といいます.
 の回りを一周するのに行なった仕事を求めてみましょう.ただし,ベクトル場は
の回りを一周するのに行なった仕事を求めてみましょう.ただし,ベクトル場は

解
 とおくと.
とおくと.


![$\displaystyle \int_{C} {\bf F} \cdot d {\bf r} = \int_{0}^{2\pi} [48 - 30\sin{t}\cos{t}]dt = 96\pi
\ensuremath{\ \blacksquare}
$](img4437.png)
 を求めてみましょう.ただし,
を求めてみましょう.ただし,  は曲線
は曲線
 の点
の点  と点
と点  を結ぶ曲線とします.
を結ぶ曲線とします.
解
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
![$\displaystyle \left[\frac{1}{5}x^{5}\right ]_{0}^{2} + \left[\frac{2}{3}x^{3} + \frac{2}{4}x^{4} \right ]_{0}^{2}$](img4443.png) |
||
 |
 |
別解
曲線  をパラメター表示すると
をパラメター表示すると


 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
![$\displaystyle \left[\frac{1}{5}t^{5} + \frac{2}{3}t^{3} + \frac{2}{4}t^{4} \right ]_{0}^{2}$](img4449.png) |
||
 |
 |
この例題で  を曲線
を曲線  の向きを
の向きを  から
から 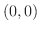 に変えた曲線とすると,
曲線
に変えた曲線とすると,
曲線  のパラメター表示は
のパラメター表示は



 とおくと,
とおくと,  より
より
 |
 |
 |
|
 |
 |
||
 |
 |


となります.
(a)
 , Cは2点
, Cは2点
 を結ぶ線分
を結ぶ線分
(b)
 , Cは2点
, Cは2点
 を結ぶ線分
を結ぶ線分
(c)
 , Cは
, Cは 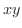 平面上の単位円の点
平面上の単位円の点 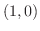 から点
から点 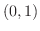 までの部分
までの部分
(d)
 , Cは原点
, Cは原点  と点
と点  を結ぶ直線
を結ぶ直線
(e)
 , Cは原点
, Cは原点  と点
と点  を
を
 に沿って結ぶ曲線
に沿って結ぶ曲線