Next: 線積分(line integrals) Up: ベクトル解析(VECTOR ANALYSIS) Previous: スカラー場とベクトル場(scalar field and vector 目次 索引
空間のある領域で定義されたベクトル場  を考えます.
を考えます.
 の成分表示を
の成分表示を

 を次のように定義します.
を次のように定義します.

ここで演算子  を用いると,div
を用いると,div
 と表わすことができます.
と表わすことができます.
 の発散を求めてみましょう.
の発散を求めてみましょう.
解
 |
 |
 |
|
 |
 |

次に,ベクトル場の発散とは何なのかを,実際の物理現象を使いながら考えてみましょう.ここでは液体,ガスなどが空間に広がっていく動きを考えます.このときその空間での粒子の速度はベクトル場
 を形成します.ここで空間の点Pを原点とする直交座標系を考え,図8.3のような
小さな直方体
を形成します.ここで空間の点Pを原点とする直交座標系を考え,図8.3のような
小さな直方体
 が液体の中にあると想像します.
が液体の中にあると想像します.
まず,直方体の中での単位時間内での質量変化を計算してみます.点  で直方体に入っていく流体の,直方体の面に垂直なベクトルの
で直方体に入っていく流体の,直方体の面に垂直なベクトルの  成分は
成分は
 ,ただし
,ただし 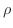 は液体の密度とします.次に直方体から出てくる流体の,直方体の面に垂直なベクトルの
は液体の密度とします.次に直方体から出てくる流体の,直方体の面に垂直なベクトルの  成分は
成分は
 |
 |
 |
|
 |
 |
||
 |
 |
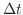 内に後ろの面から流入する物質の質量は
内に後ろの面から流入する物質の質量は


同様のことが残りの4つの面でも起こります.そこで,これらを全て加えると単位時間内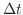 内にこの直方体
内にこの直方体
 から涌きだす質量は
から涌きだす質量は

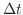 内に単位体積から涌き出す質量は
内に単位体積から涌き出す質量は

 の発散です.このことから発散は流体が単位時間内に単位体積から涌き出す質量と考えることができます.これより点Pにおいて
の発散です.このことから発散は流体が単位時間内に単位体積から涌き出す質量と考えることができます.これより点Pにおいて
 のとき涌き出し のとき涌き出し |
 のとき飲み込み のとき飲み込み |
 のとき平衡 のとき平衡 |
特に,  が保存場のとき
が保存場のとき
 は
は
 |
 |
 |
|
 |
 |
||
 |
 |
 の ラプラシアン(Laplacian)
といい,
の ラプラシアン(Laplacian)
といい,
 または
または  で表わします.また,偏微分方程式
で表わします.また,偏微分方程式

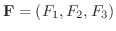 に対して
に対して  の 回転(curl),
の 回転(curl),
 を次のように定義します.
を次のように定義します.


 の回転を求めてみましょう.
の回転を求めてみましょう.
解

ベクトル場の回転を求めるのはそれほど難しくないことですが,ベクトル場の回転とは何かは分かりにくいものとなっています.そこで次の例を考えながらベクトル場の回転とは何かを理解しましょう.
 のとき,このベクトル場によって点A
のとき,このベクトル場によって点A
 , B
, B
 , C
, C
 , D
, D
 からなる四辺形ABCDをどれだけ回転させれるか調べてみます.
からなる四辺形ABCDをどれだけ回転させれるか調べてみます.
まず,点A
 での水平方向の成分は
での水平方向の成分は
 .
点D
.
点D
 での水平方向の成分は
での水平方向の成分は

 が正のとき,四辺形 ABCD は時計回りに回転します.また,点 A,Bでの垂直方向の成分の差
が正のとき,四辺形 ABCD は時計回りに回転します.また,点 A,Bでの垂直方向の成分の差
 が正のとき,四辺形 ABCD は反時計回りに回転します.よって
が正のとき,四辺形 ABCD は反時計回りに回転します.よって

 が四辺形に与える回転力の大きさとなり,その力の方向は右ねじの法則より四辺形に垂直な方向
が四辺形に与える回転力の大きさとなり,その力の方向は右ねじの法則より四辺形に垂直な方向
 となります.これがcurlの名前の由来です.このことから
となります.これがcurlの名前の由来です.このことから
 のときベクトル場
のときベクトル場  は渦なしとなります.
は渦なしとなります.
 が保存場ならば,
が保存場ならば,
 を示してみましょう.
を示してみましょう.
解
 が保存場より,
が保存場より,
 となる
となる  が存在します.よって
が存在します.よって
 を求めると
を求めると
