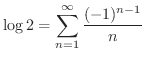Next: ベクトル関数(VECTOR FUNCTIONS) Up: 級数(SERIES) Previous: 交項級数(alternating series) 目次 索引
各項が関数であるような級数を 関数項級数(series of functions) といいます.
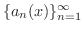 を区間
を区間  で定義された関数の列とします.この関数列
で定義された関数の列とします.この関数列
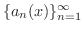 より
より
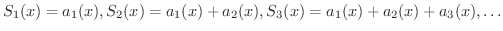
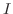 のすべての点
のすべての点  で数列
で数列
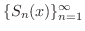 が収束するとき,つまり
が収束するとき,つまり
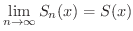
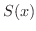 が存在するとき,級数
が存在するとき,級数
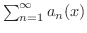 は収束するといい,
は収束するといい, 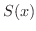 を無限級数の和とよびます.特に収束が区間
を無限級数の和とよびます.特に収束が区間 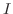 において一様収束である場合,つまり,
において一様収束である場合,つまり, 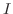 の任意の
の任意の  に対して
に対して
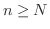 ならば
ならば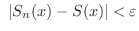
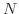 が
が 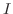 の
の  に無関係に存在する場合,級数
に無関係に存在する場合,級数
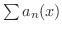 は
は 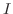 で一様収束する(uniformly convergent) といいます.
で一様収束する(uniformly convergent) といいます.
ここで
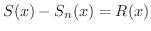 とおくと,無限級数の一様収束は次のように表わせます.
とおくと,無限級数の一様収束は次のように表わせます.
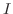 の任意の
の任意の  に対して
に対して
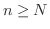 ならば
ならば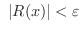
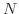 が存在する.
が存在する.
次に,ドイツの数学者 Carl Weierstrass (1815-1897) によって示された一様収束するための簡単な十分条件を学びます.
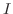 の任意の
の任意の  に対して
に対して
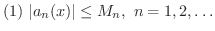
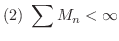
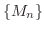 が存在するとき,
が存在するとき,
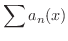 は
は  で一様収束かつ絶対収束である.
で一様収束かつ絶対収束である.
証明
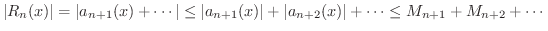
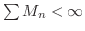 より,どんな
より,どんな
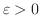 に対しても
に対しても 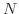 が存在し,
が存在し, 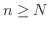 ならば
ならば
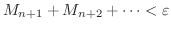
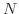 は明らかに
は明らかに  とは無関係なので,
とは無関係なので, 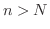 のとき
のとき
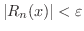 が成り立ちます.
が成り立ちます.

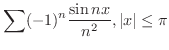 は一様収束するか調べてみましょう.
は一様収束するか調べてみましょう.
解
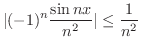 . また
. また
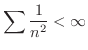 なので,Weierstrassの判定法により一様収束します.
なので,Weierstrassの判定法により一様収束します.

ここでなぜ一様収束という考え方が生まれたのか考えてみましょう.例えば
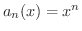 となる級数
となる級数
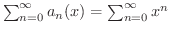 を考えます.関数列
を考えます.関数列
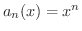 は区間
は区間
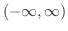 で連続です.すると定理1.4より
で連続です.すると定理1.4より
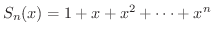 も区間
も区間
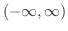 で連続となります.そこでその極限値
で連続となります.そこでその極限値
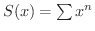 も連続だろうと考えたくなります.しかし,実際はどうでしょう.
も連続だろうと考えたくなります.しかし,実際はどうでしょう.
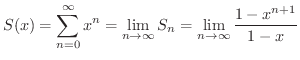
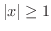 のときには,発散してしまいます.つまり,たとえすべての項が連続でもその和は連続とは限らないのです.これでは不便なので,なんとか有限のときに成り立つ性質を,無限のときにも適用できるように,考え出されたのが一様収束という概念なのです.よって無限級数が一様収束するとき,級数は有限級数のもっている多くの性質を継承します.
のときには,発散してしまいます.つまり,たとえすべての項が連続でもその和は連続とは限らないのです.これでは不便なので,なんとか有限のときに成り立つ性質を,無限のときにも適用できるように,考え出されたのが一様収束という概念なのです.よって無限級数が一様収束するとき,級数は有限級数のもっている多くの性質を継承します.
 が区間
が区間 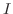 で連続で
で連続で
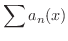 が
が 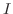 で一様収束ならば,
で一様収束ならば,
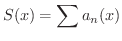 も
も 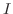 で連続である.
で連続である.
証明
区間Iの任意の点  に対して,
に対して,
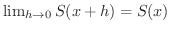 がいえればよいでしょう.まず,一様収束の仮定に着目し,
がいえればよいでしょう.まず,一様収束の仮定に着目し,
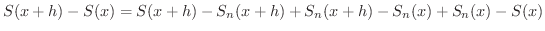
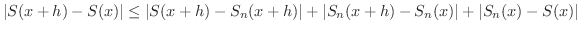
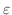 に対し,
に対し, 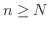 ならば
ならば
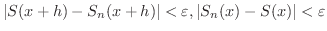
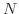 が存在します.
次に
が存在します.
次に 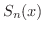 の連続性から,
の連続性から,
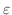 に対し
に対し 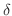 を適当にとることができ,
を適当にとることができ,
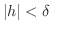 ならば
ならば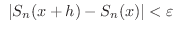
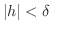 ならば
ならば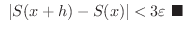
 が区間
が区間 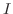 で連続で
で連続で
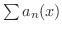 が
が 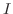 で一様収束ならば,
で一様収束ならば,
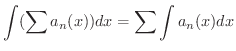
証明 区間 ![$I = [a,b]$](img2877.png) 内の任意の点
内の任意の点  に対して,
に対して,
![$\displaystyle \vert\int_{a}^{x} S_{n}(x)dx - \int_{a}^{x}S(x)dx\vert = \vert\in...
...}^{x}[S_{n}(x) - S(x)]dx \vert \leq \int_{a}^{x} \vert S_{n}(x) - S(x)\vert dx $](img2878.png)
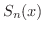 が
が 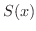 に一様収束するので,任意の正の数
に一様収束するので,任意の正の数
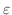 に対し,
に対し,  に無関係に
に無関係に 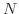 をとり,
をとり, 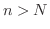 ならば,
ならば,
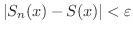 とすることができるはずです.したがって,
とすることができるはずです.したがって, ![$[a,b]$](img158.png) の任意の
の任意の  について,
について, 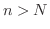 ならば,
ならば,
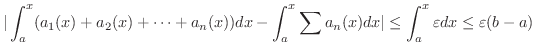
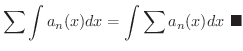
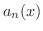 が区間
が区間 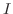 で
で 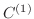 級で,
級で,
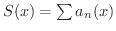 かつ
かつ
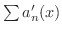 が一様収束するならば
が一様収束するならば
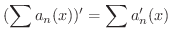
証明
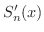 が一様収束するので,その極限関数を
が一様収束するので,その極限関数を 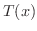 とおくと,前の2つの定理より,
とおくと,前の2つの定理より, 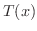 は連続で,
は連続で,
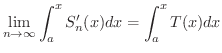
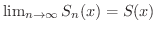 に注意すると,
に注意すると,
![$\displaystyle \lim_{n \rightarrow \infty} \int_{a}^{x} S_{n}^{\prime}(x) dx = \lim_{n \rightarrow \infty} [S_{n}(x) - S_{n}(a)] = S(x) - S(a)$](img2890.png)
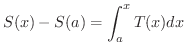
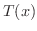 は連続なので,
は連続なので,
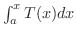 は微分可能でかつ
は微分可能でかつ
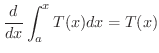
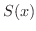 も微分可能で,
も微分可能で,
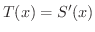 となり,これより
となり,これより
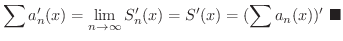
無限級数
 において,特に
において,特に
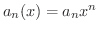 のときを 整級数(power series) といいます.例えば
のときを 整級数(power series) といいます.例えば
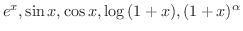 のTaylor級数
のTaylor級数
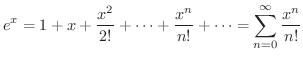 |
|||
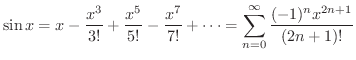 |
|||
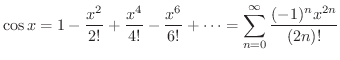 |
|||
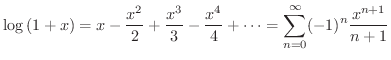 |
|||
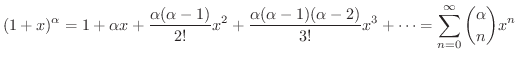 |
は整級数の1つです.ここで,
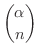 は
は
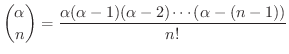 を意味し一般化された2項係数といいます.
を意味し一般化された2項係数といいます.
さて
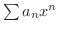 は
は  のどんな値に対して収束するのでしょうか.
のどんな値に対して収束するのでしょうか.
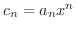 とおき, D'Alembert の判定法を用いると
とおき, D'Alembert の判定法を用いると
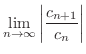 |
 |
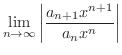 |
|
 |
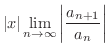 |
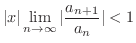 ならば
ならば
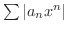 は収束し,
は収束し,
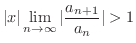 ならば
ならば
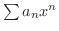 は発散するのでこの極限値
は発散するのでこの極限値
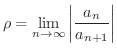
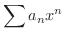 は
は
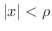 のとき絶対収束し,
のとき絶対収束し,
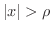 のとき発散する.
のとき発散する.
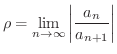 を用いて次の整級数の収束半径を求めてみましょう.
を用いて次の整級数の収束半径を求めてみましょう.
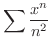
解
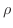 |
 |
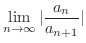 |
|
 |
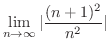 |
||
 |
 |
次に整級数の基本性質をあげておきます.
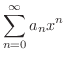 の収束半径を
の収束半径を 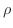 とし,
とし,
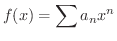 とおくと,次の
とおくと,次の 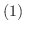 から
から 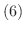 が成り立つ.
が成り立つ.
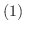 任意の
任意の
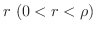 に対し,
に対し,
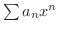 は
は ![$[-r,r]$](img2929.png) で絶対収束かつ一様収束する.
で絶対収束かつ一様収束する.
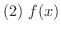 は
は
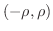 で連続である.
で連続である.
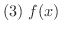 は
は
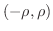 で項別積分可能であって,次の式が成り立つ.
で項別積分可能であって,次の式が成り立つ.
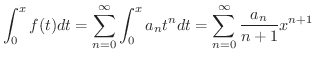
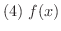 は
は
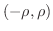 で項別微分可能であって,次の式が成り立つ.
で項別微分可能であって,次の式が成り立つ.
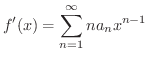
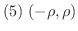 において
において  の Taylor級数は整級数
の Taylor級数は整級数
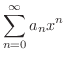 である.つまり
である.つまり
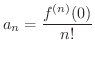
証明
(1)
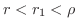 を満たす
を満たす 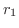 をとると,定理4.4より
をとると,定理4.4より
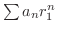 は絶対収束します.そこで
は絶対収束します.そこで
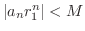 となる
となる 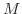 を適当にとることができる.したがって,
を適当にとることができる.したがって,
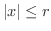 ならば,
ならば,
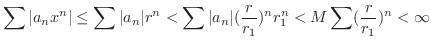
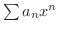 は
は ![$[-r,r]$](img2929.png) で絶対収束かつ一様収束します.
で絶対収束かつ一様収束します.
(2)
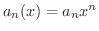 とおくと,無限級数の連続性により,
とおくと,無限級数の連続性により,  は
は
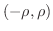 で連続となる.
で連続となる.
(3)
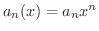 とおくと,項別積分の定理により,
とおくと,項別積分の定理により,
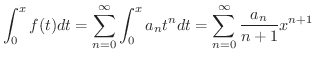
(4)
 の収束半径を求めると
の収束半径を求めると
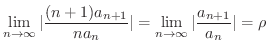
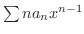 は
は ![$[-r,r]$](img2929.png) で一様収束するので,項別微分の定理より
で一様収束するので,項別微分の定理より
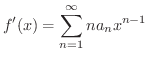
(5)  のTaylor級数を求めると
のTaylor級数を求めると
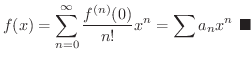
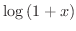 の整級数を求めてみましょう.
の整級数を求めてみましょう.
解
Taylor展開すれば整級数は求まりますが,もっと簡単に求めることができます.
まず,
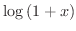 は
は
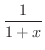 の不定積分であることを思い出します.つまり,
の不定積分であることを思い出します.つまり,
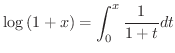
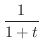 を級数展開すると
を級数展開すると
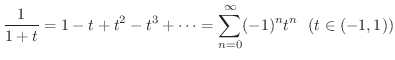
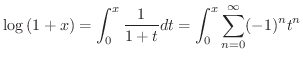
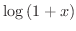 |
 |
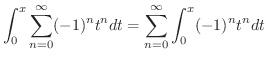 |
|
 |
![$\displaystyle \sum_{n=0}^{\infty} \left[\frac{(-1)^{n} t^{n+1}}{n+1} \right]_{n...
...} \frac{(-1)^{n} x^{n+1}}{n+1} = \sum_{n=1}^{\infty} \frac{(-1)^{n-1} x^{n}}{n}$](img2955.png) |
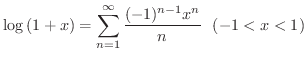
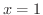 のときどうなるか考えてみましょう.
のときどうなるか考えてみましょう.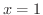 のとき,右辺はLeibnizの定理の条件を満たす交項級数となるので収束します.よって
のとき,右辺はLeibnizの定理の条件を満たす交項級数となるので収束します.よって