Next: 部分積分法(integration by parts) Up: 積分法(INTEGRATION) Previous: 不定積分(indefinite integrals) 目次 索引
不定積分
 を求めるときに,被積分関数
を求めるときに,被積分関数  の原始関数が四則の演算により積分公式(1)から(12)の形に直せないことがよくあります.そんなとき,
の原始関数が四則の演算により積分公式(1)から(12)の形に直せないことがよくあります.そんなとき,  の
の  をある
をある 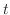 の関数
の関数  に置き換えることにより,
に置き換えることにより,  を
を
 という,公式(1)から(12)を用いることにより積分できる形に変形することを 置換積分法(integration by substitution) といいます.
という,公式(1)から(12)を用いることにより積分できる形に変形することを 置換積分法(integration by substitution) といいます.
 が連続であるとき,
が連続であるとき,
 とおくと,
とおくと,  が微分可能であれば,
が微分可能であれば,

証明
 とすると,
とすると,
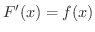 である.そこで
である.そこで
 とおき,
とおき,
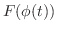 を考えると,
を考えると,



この定理により,
 を求めるのに,
を求めるのに,
 とその微分
とその微分
 とをもとの式に形式的に代入し,
とをもとの式に形式的に代入し,
 としてこれを計算すればよいことがわかります.
としてこれを計算すればよいことがわかります.
 を求めてみましょう.
を求めてみましょう.
解
このままの形では,公式(1)から(12)のどれも使えないことがわかります.そこで
 とおきます.すると
とおきます.すると
 となるので,これを用いて元の不定積分を書き直すと
となるので,これを用いて元の不定積分を書き直すと

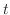 が用いられています.よって
が用いられています.よって


この例題に用いたテクニックを一般化すると次の公式を得ます.

この公式を用いると


 を求めてみましょう.
を求めてみましょう.
解
 とおくと,
とおくと, 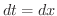 .また
.また  より,
より,
 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
 を求めてみましょう.
を求めてみましょう.
解
 とおくと,
とおくと,
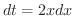 となるので,
となるので,
 |
 |
 |
|
 |
 |