Next: 同値関係 Up: 群 Previous: 群の定義 目次 索引
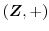 : 有理整数の全体は加法に対して群になることを示せ.
: 有理整数の全体は加法に対して群になることを示せ.
解
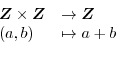 という対応は写像である.
という対応は写像である.
(G1) 結合法則
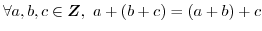 |
(G2) 単位元
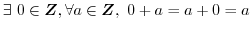 |
(G3) 逆元の存在
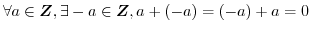 |
よって,有理整数全体
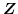 は演算
は演算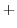 に対して群になる.
に対して群になる.
![${\mathcal Q}[\sqrt{2}] = \{a + b\sqrt{2}: a,b \in {\mathcal Q}\}$](img42.png) から0を除いた集合
から0を除いた集合
![${\mathcal Q}[\sqrt{2}]^*$](img43.png) は乗法に関して群になることを示せ.
は乗法に関して群になることを示せ.
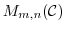 を
を
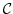 の元を成分とする
の元を成分とする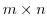 型行列全体の集合とする.このとき,
型行列全体の集合とする.このとき,
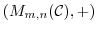 は加法群になることを示せ.
は加法群になることを示せ.
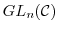 を
を
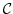 の元を成分とする
の元を成分とする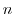 次正則行列全体の集合とする.このとき,
次正則行列全体の集合とする.このとき,
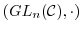 は乗法群になることを示せ.
は乗法群になることを示せ.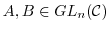 とするとき,
とするとき,
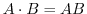 . これは,2項演算である.なぜならば,
. これは,2項演算である.なぜならば,
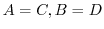 のとき,
のとき,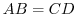 .
次に,
.
次に,
(G1) 結合法則:
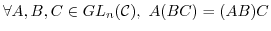
(G2) 単位元:
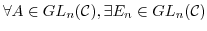 (
(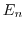 は
は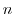 次の単位行列),
次の単位行列),
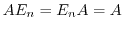
(G3) 逆元の存在:
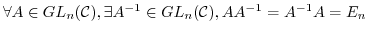
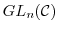 を
を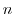 次一般線形群という.
次一般線形群という.
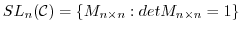 を
を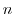 次特殊線形群という.
次特殊線形群という.
 に属する全ての元
に属する全ての元 に対して,
に対して,
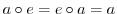 を満たす
を満たす の元
の元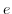 は唯一つである.
は唯一つである.
 に属する任意の元
に属する任意の元 に対して,
に対して,
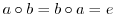 を満たす
を満たす の元
の元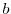 は
は により一意的に定まる.
により一意的に定まる.
 が群であるとする.このとき,
が群であるとする.このとき, に属する任意の2つの元
に属する任意の2つの元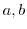 に対して,
に対して,
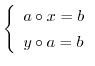
 の元
の元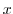 および
および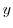 が存在し,しかも,唯一通りに定まる.
が存在し,しかも,唯一通りに定まる.証明 一意性の証明と存在の証明を行う必要がある.
 においては,消去律がなりたつ.すなわち,群
においては,消去律がなりたつ.すなわち,群 に属する任意の元
に属する任意の元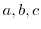 について
について
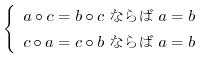
証明 各自に任せる.
 を有限集合とする.
を有限集合とする. が群であるための必要十分条件は
が群であるための必要十分条件は
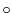 が定義されている
が定義されている
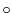 に関して結合法則が成り立つ
に関して結合法則が成り立つ
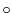 に関して消去律が成り立つ
に関して消去律が成り立つ