Next: 群の例 Up: 群 Previous: 群 目次 索引
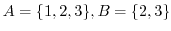 の直積集合を求めよ.
の直積集合を求めよ.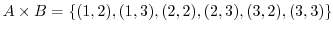
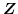 を整数全体の集合,
を整数全体の集合,
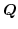 を有理数全体の集合,
を有理数全体の集合,
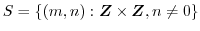 とする.このとき,
とする.このとき,
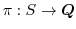 を
を
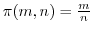 と定義すると,
と定義すると,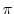 は写像である.
は写像である.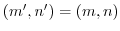 とすると,直積の定義より,
とすると,直積の定義より,
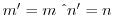 .よって,
.よって,
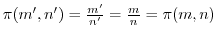 となり,
となり,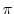 は写像である.
は写像である.
 の直積集合から
の直積集合から への写像を
への写像を の2項演算(binary operation)という.
の2項演算(binary operation)という.
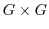 の元
の元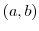 の写像による像を
の写像による像を と
と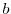 の積といい,記号
の積といい,記号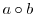 または
または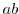 で表す.また,このとき,集合
で表す.また,このとき,集合 に1つの2項演算が与えられているといい,
に1つの2項演算が与えられているといい,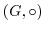 と表す.
と表す.
 は空でない集合とする.
は空でない集合とする. に2項演算が与えられていて,次の条件を満たすとき,
に2項演算が与えられていて,次の条件を満たすとき, はこの演算に関して群(group)であるという.
はこの演算に関して群(group)であるという.
(G1) 結合法則
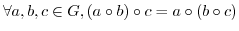 |
(G2) 単位元の存在
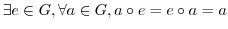 |
(G3) 逆元の存在
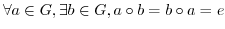 |
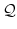 に2項演算
に2項演算
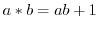 が与えられている.このとき,2項演算
が与えられている.このとき,2項演算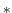 は結合法則を満たすか調べよ.
は結合法則を満たすか調べよ.
 に属する任意の元
に属する任意の元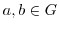 に対して,
に対して,
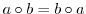 が成り立つとき,
が成り立つとき, を可換群,または,アーベル群という.
を可換群,または,アーベル群という.
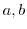 を群
を群 の元とする.
の元とする. と
と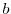 が可換であるとき,
が可換であるとき,
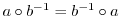 が成り立つことを示せ.
が成り立つことを示せ.