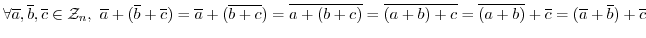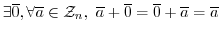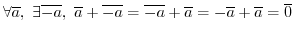Next: 群表 Up: 群 Previous: 群の例 目次 索引
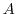 の直積集合
の直積集合
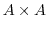 の部分集合
の部分集合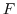 が与えられているとする.
が与えられているとする.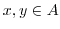 であって
であって
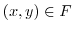 であるとき,
であるとき,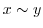 と書き,
と書き,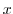 と
と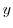 は
は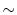 という関係にあるという.特に,次の3つの条件を満たすものを同値関係(equivalence relation)という.
という関係にあるという.特に,次の3つの条件を満たすものを同値関係(equivalence relation)という.
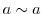
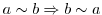
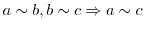
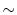 を同値関係とする.
を同値関係とする.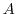 の元
の元 に同値である
に同値である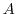 の元全体を
の元全体を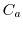 で表して,
で表して,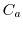 を
を の同値類(equivalence class)といい,
の同値類(equivalence class)といい, を同値類
を同値類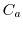 の代表元という.
の代表元という.
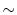 を
を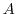 上の同値関係とする.すべての同値類から1つずつ元を選んで集めた集合を
上の同値関係とする.すべての同値類から1つずつ元を選んで集めた集合を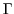 とする.このとき,全ての
とする.このとき,全ての
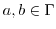 に対して,
に対して,
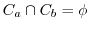 ならば,
ならば,
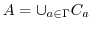 と表せる.逆に,
と表せる.逆に,
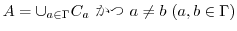 ならば
ならば 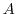 上に同値関係を構築することができる.
上に同値関係を構築することができる.
つまり,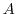 上に同値関係があれば,もとの集合
上に同値関係があれば,もとの集合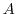 は同値類
は同値類
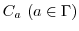 によって分割される.このことを集合
によって分割される.このことを集合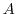 は同値関係
は同値関係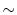 によって類別されるといい,
によって類別されるといい,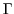 をこの同値関係
をこの同値関係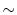 の完全代表系という
の完全代表系という
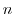 は1より大きい整数,
は1より大きい整数,
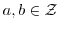 に対して,
に対して,
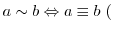 mod
mod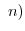 と定義すると,
と定義すると,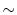 は同値関係であることを示せ.また,同値類
は同値関係であることを示せ.また,同値類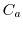 を求めよ.このとき,
を求めよ.このとき,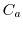 は剰余類という.
は剰余類という.
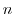 を法とする剰余類の集合を
を法とする剰余類の集合を
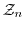 で表すと,
で表すと,
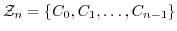
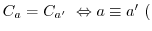 mod
mod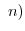 を示せ.
を示せ.
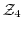 を考える.
を考える.
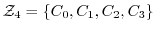
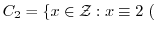 mod
mod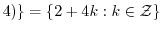 と表せるので,
と表せるので,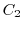 と書く代わりに
と書く代わりに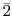 で表すことにする.すると,
で表すことにする.すると,
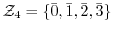 と表せる.
と表せる.
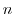 を法とする剰余類の集合
を法とする剰余類の集合
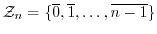 には,
には,
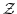 の演算から自然に演算が導入される.すなわち,
の演算から自然に演算が導入される.すなわち,
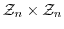 の元
の元
 に
に
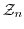 の元
の元
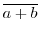 を対応させると写像を与えることを示せ.
を対応させると写像を与えることを示せ.
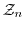 は上で定めた加法
は上で定めた加法
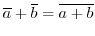 により群になる.
により群になる.