Next: 部分群による類別 Up: 群 Previous: 群の位数,元の位数 目次 索引
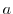 を群
を群 の元とするとき,
の元とするとき,
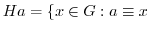 mod
mod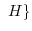
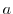 の位数が無限である場合:
の位数が無限である場合:
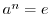 となる正の整数は存在しない.したがって,
となる正の整数は存在しない.したがって,
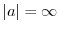 となる.次に,集合
となる.次に,集合
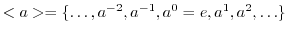 を考える.このとき,
を考える.このとき,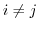 ならば,
ならば,
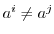 である.もし,
である.もし,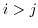 で
で
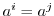 とすると,
とすると,
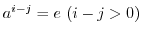 となり,
となり,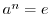 となる正の整数は存在しないと矛盾する.したがって,
となる正の整数は存在しないと矛盾する.したがって,
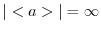 .
.
(2) 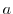 の位数が有限の場合:
の位数が有限の場合:
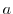 の位数を
の位数を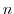 とすると,
とすると,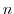 は最小の正の整数で
は最小の正の整数で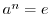 である.ここで,
である.ここで,
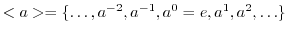 を考える.このとき,
を考える.このとき,
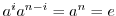 に注意すると,
に注意すると,
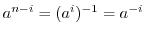 .したがって,
.したがって,
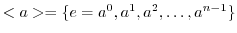 .よって,
.よって,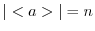 .
.
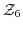 の元
の元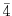 の位数と
の位数と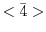 の位数を求めよ.
の位数を求めよ.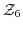 は加法群である.したがって,単位元は
は加法群である.したがって,単位元は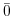 で,
で,
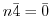 となる最小の正の整数
となる最小の正の整数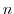 を求めると,
を求めると,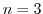 となる.
また,
となる.
また,
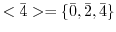 より,
より,
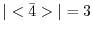
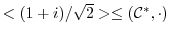 の位数を求めよ.
の位数を求めよ.
 の元を
の元を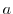 とするとき,
とするとき,
 であることを示せ..
であることを示せ..
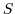 を群
を群 の部分集合とする.このとき,
の部分集合とする.このとき,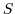 を含む
を含む の部分群のすべての共通部分
の部分群のすべての共通部分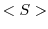 は
は の部分群になる(定理3.2).この
の部分群になる(定理3.2).この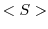 を
を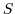 により生成された
により生成された の部分群といい,
の部分群といい,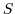 を
を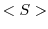 の生成系という.
の生成系という.
 を群として,
を群として,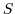 をその空でない部分集合とする.このとき,
をその空でない部分集合とする.このとき,
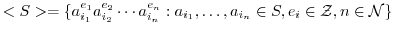
証明 右辺を とおいて,
とおいて,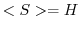 を示す.
を示す.
i)
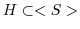 を示す:
を示す:
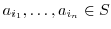 であり,
であり,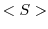 は群であるから
は群であるから
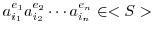 .ゆえに,
.ゆえに,
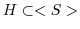 .
.
ii)
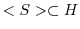 を示す:
を示す:
定義より,
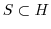 である.ここで,
である.ここで,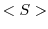 は
は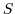 を含む最小の群であることを示す.もし,
を含む最小の群であることを示す.もし,
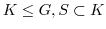 とすると,
とすると,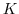 が群であるから,
が群であるから,
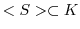 . これより,
. これより, が群であることを示せばよいことが分かる.
が群であることを示せばよいことが分かる.
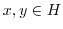 とすると,
とすると,
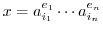 ,
,
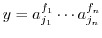 .これより,
.これより,
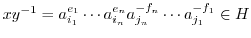 .よって,
.よって,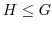 .
.
 が加法群のとき,
が加法群のとき,
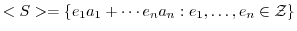
 の部分集合を
の部分集合を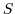 とするとき次を示せ.
とするとき次を示せ.
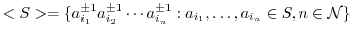
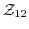 の部分集合
の部分集合
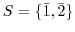 によって生成された部分群を調べてみよう.
によって生成された部分群を調べてみよう.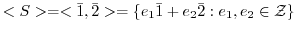 より,
より,
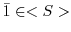 .したがって,
.したがって,
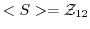
 の部分集合
の部分集合
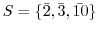 によって生成された部分群を調べよ.
によって生成された部分群を調べよ.
 を
を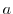 によって生成される位数
によって生成される位数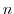 の巡回群とする.このとき,
の巡回群とする.このとき, の元
の元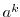 の位数は
の位数は
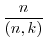 となる.ただし,
となる.ただし,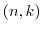 は
は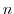 と
と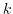 の最大公約数を表す.
の最大公約数を表す.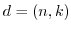 とすると,
とすると,
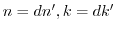 より
より
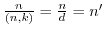 .したがって,
.したがって,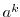 の位数が
の位数が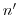 であることを示せばよい.
であることを示せばよい.
(1)
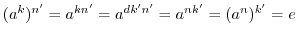
(2) 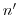 が
が
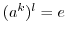 となる最小の正の整数であることを示す.もし,
となる最小の正の整数であることを示す.もし,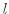 が
が
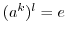 を満たす最小の正の整数とすると,
を満たす最小の正の整数とすると,
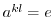 より,
より,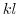 は
は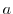 の位数で割り切れる.よって,
の位数で割り切れる.よって,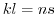 .ここで,
.ここで,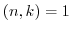 より
より
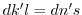 .したがって,
.したがって,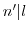 .
.
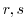 を自然数とする.群
を自然数とする.群 の元
の元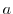 の位数を
の位数を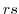 とすると,元
とすると,元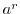 の位数は
の位数は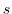 であり,元
であり,元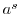 の位数は
の位数は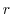 である.
である.
(1)
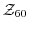 において,元
において,元
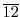 と
と
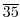 の位数を求めよ.
の位数を求めよ.
 を
を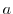 によって生成される位数
によって生成される位数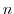 の巡回群とする.このとき,
の巡回群とする.このとき, の元
の元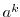 が
が の生成元であるための必要十分条件は,
の生成元であるための必要十分条件は,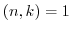 となることである.
となることである.
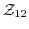 の生成元を調べよ.
の生成元を調べよ.
 の2つの元
の2つの元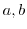 が可換で,位数が,それぞれ
が可換で,位数が,それぞれ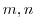 とする.このとき,
とする.このとき,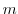 と
と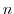 が互いに素であれば元
が互いに素であれば元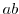 の位数は
の位数は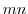 である.
である.
(1)
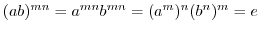 .
.
(2)
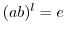 とすると,
とすると,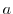 と
と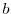 は可換であるから,
は可換であるから,
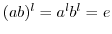 .ゆえに,
.ゆえに,
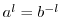 .両辺を
.両辺を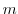 乗すると
乗すると
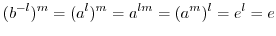
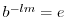 より
より
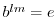 .
.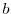 の位数は
の位数は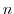 なので,
なので,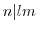 .このとき,
.このとき,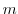 と
と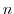 は互いに素なので,
は互いに素なので,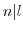 .同様にして,
.同様にして,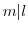 を得る.よって,
を得る.よって,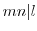 より,
より,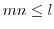 .
.