Next: 索引 Up: 群 Previous: 巡回群,生成群 目次 索引
 を群,
を群, を
を の部分群とする.
の部分群とする.
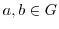 に対して,
に対して,
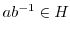 のとき,
のとき,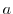 と
と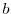 は
は を法として右合同であるといい,
を法として右合同であるといい,
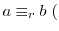 mod
mod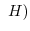
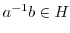 のとき,
のとき,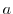 と
と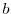 は
は を法として左合同であるといい,
を法として左合同であるといい,
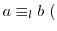 mod
mod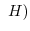
証明 (1) 反射率,(2) 対称律,(3) 推移律が成り立つことを示す. (1)
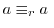 mod
mod を示す.そのためには,
を示す.そのためには,
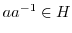 を示せばよい.
を示せばよい. は群で,
は群で,
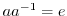 より,
より,
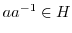 .
.
(2)
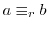 mod
mod ならば
ならば
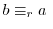 mod
mod を示す.
を示す.
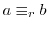 mod
mod とすると,
とすると,
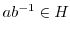 .示したいのは,
.示したいのは,
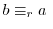 mod
mod .つまり,
.つまり,
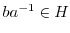 .
. は群なので,
は群なので,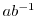 の逆元
の逆元
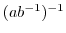 も
も の元である.ところで,例題4.1より
の元である.ところで,例題4.1より
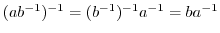 .したがって,
.したがって,
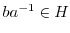
(3)
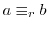 mod
mod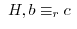 mod
mod ならば,
ならば,
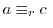 mod
mod を示せばよい.各自に任せる.
を示せばよい.各自に任せる.
 を群,
を群, を
を の部分群,
の部分群,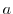 を
を の元とするとき,
の元とするとき,
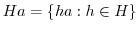 を
を の右剰余類という.
の右剰余類という.
証明
![$[a] = \{x \in G : a \equiv_{r} x \ $](img411.png) mod
mod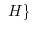 とする.まず,
とする.まず,
![$Ha \subset [a]$](img413.png) を示す.つまり,
を示す.つまり,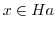 のとき,
のとき,![$x \in [a]$](img415.png) を示せばよい.言い換えると,
を示せばよい.言い換えると,
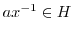 を示せばよい.
を示せばよい.
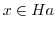 とすると,
とすると,
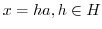 .
. は群なので,
は群なので,
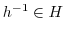 .したがって,
.したがって,
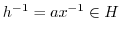 .
.
次に,
![$[a] \subset Ha$](img420.png) を示す.
を示す.![$x \in [a]$](img415.png) とすると,
とすると,
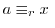 mod
mod .つまり,
.つまり,
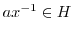 .
. は群なので,
は群なので,
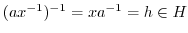 .したがって,
.したがって,
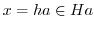 .
.
定理1.17により,![$[a]$](img424.png) は同値類,定理1.18により
は同値類,定理1.18により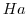 は同値類であることが分かる.したがって,
は同値類であることが分かる.したがって, は共通部分を持たない同値類により分割される.よって,すべての
は共通部分を持たない同値類により分割される.よって,すべての を法とする右剰余類は互いに等しいか共通部分を持たない.まとめると,
を法とする右剰余類は互いに等しいか共通部分を持たない.まとめると,
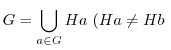 ならば
ならば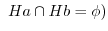
 の
の による右類別という.
による右類別という.
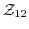 の部分群
の部分群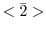 による右剰余類の集合を調べてみよう.
による右剰余類の集合を調べてみよう.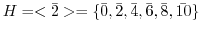 .
.
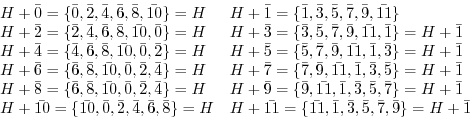
確かに,
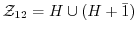 となっている.
となっている.
ここで,それぞれの剰余類の濃度が同じであることに気づいただろうか.実は,次の定理が成り立つ.
 を群,
を群, を部分群とするとき,
を部分群とするとき, の右剰余類の集合の濃度はすべて等しい.
の右剰余類の集合の濃度はすべて等しい.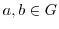 のとき
のとき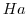 と
と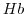 の濃度が等しいことを示せばよい.そこで,
の濃度が等しいことを示せばよい.そこで,
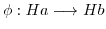 を考える.
を考える.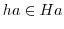 に対して,
に対して,
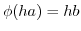 とおくと,
とおくと,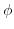 は全射である.つぎに,
は全射である.つぎに,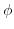 が単射であることを示す.各自に任せる.
が単射であることを示す.各自に任せる.
この定理より,次の定理の証明ができる.
 を有限群,
を有限群, を
を の部分群とすると,
の部分群とすると, の位数は
の位数は の位数の約数である.
の位数の約数である. を法とする
を法とする の右剰余類による
の右剰余類による の類別を行うと,
の類別を行うと,
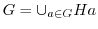
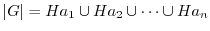
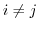 ならば
ならば
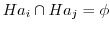 より,
より,
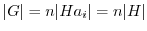 .
.
 を群,
を群, を
を の部分群とするとき,
の部分群とするとき, の右剰余類の集合の濃度を
の右剰余類の集合の濃度を における
における の指数といい,
の指数といい,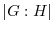 で表す.
で表す.Lagrangeの定理より,
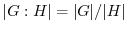
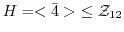 とするとき,
とするとき, による右剰余類をすべて求めよ.
による右剰余類をすべて求めよ.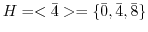 より,
より, .次に,
.次に, による右剰余類を求めると,
による右剰余類を求めると,
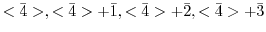
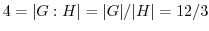 が成り立つことが分かる.
が成り立つことが分かる.
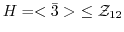 とするとき,Lagrangeの定理が成り立つことを確かめよ.
とするとき,Lagrangeの定理が成り立つことを確かめよ.
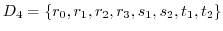 の部分群
の部分群
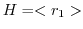 について,Lagrangeの定理が成り立つことを確かめよ.
について,Lagrangeの定理が成り立つことを確かめよ.