Next: 巡回群,生成群 Up: 群 Previous: 一般結合法則 目次 索引
 に属する元の個数を
に属する元の個数を の位数(order)といい,記号
の位数(order)といい,記号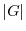 で表す.
で表す. が無限群のときは
が無限群のときは
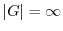 とする.
とする.
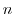 次の交代群
次の交代群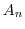 の位数を求めよ.
の位数を求めよ.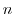 次の対称群
次の対称群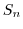 の位数は,
の位数は,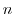 個の元を
個の元を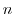 個の元に移す写像の個数であるから,順列の数である.したがって,
個の元に移す写像の個数であるから,順列の数である.したがって,
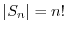 .次に,
.次に,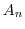 は
は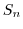 の偶置換の集合であるから,
の偶置換の集合であるから,
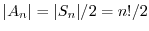 .
.
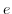 とする群
とする群 の元
の元 に対して,
に対して,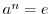 となるような最小の正の整数を
となるような最小の正の整数を の位数という.そのような整数がないとき,
の位数という.そのような整数がないとき, の位数は無限という.
の位数は無限という. の位数も記号
の位数も記号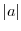 で表す.
で表す.
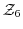 の元
の元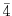 の位数を求めよ.
の位数を求めよ.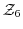 は加法群である.したがって,単位元は
は加法群である.したがって,単位元は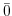 で,
で,
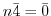 となる最小の正の整数
となる最小の正の整数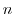 を求めると,
を求めると,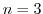 となる.
となる.
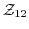 の各元の位数を求めよ.
の各元の位数を求めよ.
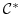 において,純虚数
において,純虚数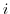 の位数を求めよ.
の位数を求めよ.
 の元
の元 からなる集合
からなる集合
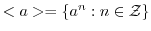 は
は の部分群になる.また,この群は
の部分群になる.また,この群は を含む
を含む の最小の部分群である.
の最小の部分群である.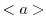 が
が の部分群であることを示す.
の部分群であることを示す.
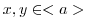 とおくと,
とおくと,
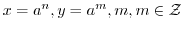 .ここで,
.ここで,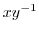 が
が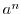 の形をしていることを示せばよい.
の形をしていることを示せばよい.
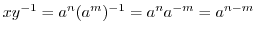 より,
より,
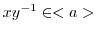 .
.
次に,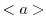 が
が を含む
を含む の最小の部分群であることを示す.すでに,
の最小の部分群であることを示す.すでに,
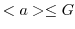 は示したので,最小の部分群であることを示せばよい.最小であることを示すには,他に
は示したので,最小の部分群であることを示せばよい.最小であることを示すには,他に を含む部分群があると仮定し,この群が
を含む部分群があると仮定し,この群が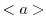 を含むことを示せばよい.そこで,
を含むことを示せばよい.そこで,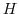 を
を の元
の元 を含む部分群とすると,
を含む部分群とすると,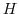 は部分群より全ての
は部分群より全ての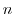 に対して
に対して
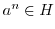 となる.したがって,
となる.したがって,
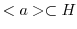 .
.
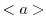 を
を で生成された
で生成された の巡回部分群(cyclic subgroup)という.
の巡回部分群(cyclic subgroup)という.
 のすべての元が
のすべての元が のある元
のある元 の累乗になっているとき,
の累乗になっているとき, は
は で生成された巡回群(cyclic group)であるといい,
で生成された巡回群(cyclic group)であるといい, をその生成元という.
をその生成元という.
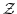 は1と
は1と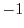 を生成元とする巡回群であることを示せ.
を生成元とする巡回群であることを示せ.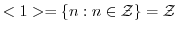 ,
,
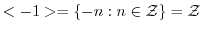 .
.
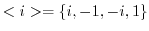 は
は
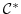 の巡回部分群であることを示せ.
の巡回部分群であることを示せ.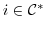 より,
より,
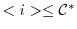 .
.
 の単位元を
の単位元を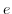 とし,
とし, の元
の元 の位数を
の位数を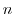 とする.このとき,非負整数について次が成り立つ.
とする.このとき,非負整数について次が成り立つ.
 mod
mod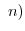
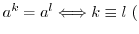 mod
mod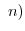
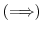
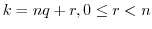 .ここで,
.ここで,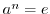 より,
より,
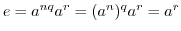 .したがって,
.したがって,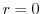 .すなわち,
.すなわち,
 mod
mod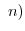
(1)
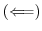
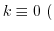 mod
mod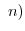 より,
より,
 . したがって,
. したがって,
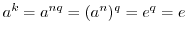
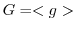 ,
,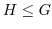 とする.
とする.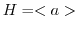 であることを示す.
であることを示す.
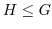 とすると
とすると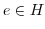 より,
より,
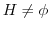 .
.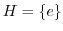 は巡回群であるので,
は巡回群であるので,
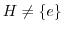 とする.
とする. を
を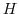 の元とすると,
の元とすると,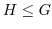 より,
より,
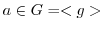 .よって,ある整数
.よって,ある整数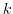 で
で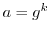 である.ここで,
である.ここで,
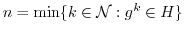 とする.このとき,
とする.このとき,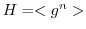 であることを示す.
であることを示す.
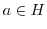 とすると,
とすると,
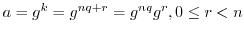 より,
より,
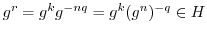 .したがって,
.したがって,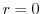 .ゆえに,
.ゆえに,
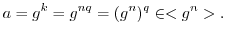
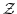 と
と
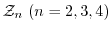 について,その部分群を調べよ.
について,その部分群を調べよ.
=2.6zw =1
(1)
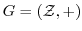
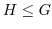 とすると,
とすると,
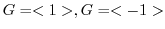 より,
より,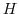 は巡回群である.そこで,
は巡回群である.そこで,
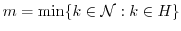 とおくと,
とおくと,
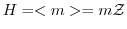 となる.
となる.
(2)
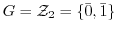
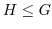 とすると,
とすると,
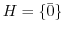 または
または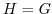 となり,
となり, は真部分群を持たない.
は真部分群を持たない.
(3)
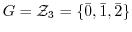
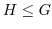 とすると,
とすると,
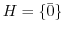 または
または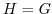 となり,
となり, は真部分群を持たない.
は真部分群を持たない.
=2.6zw =1
(4)
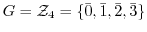
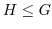 とすると,
とすると,
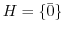 ,
,
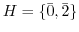 ,
, 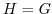 となり,
となり, の真部分群は
の真部分群は
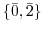 . これを次のように描く.
. これを次のように描く.
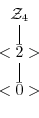
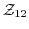 の部分群を調べよ.
の部分群を調べよ.
 を軍,
を軍,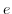 をその単位元とする.
をその単位元とする. が真部分集合をもたなければ,
が真部分集合をもたなければ, は位数が素数
は位数が素数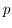 の巡回群であることを示せ.
の巡回群であることを示せ.
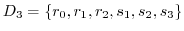 の部分群を調べよ.
の部分群を調べよ.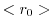 |
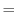 |
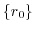 |
|
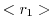 |
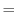 |
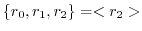 |
|
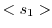 |
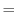 |
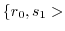 |
|
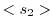 |
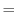 |
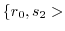 |
|
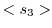 |
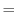 |
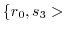 |
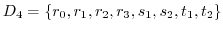 の部分群を調べよ.
の部分群を調べよ.