Next: 群の位数,元の位数 Up: 群 Previous: 部分群 目次 索引
 の元
の元
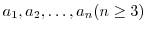 について,積
について,積
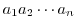 を帰納的に次のように定義する.
を帰納的に次のように定義する.
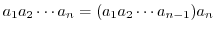
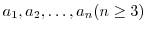 を群
を群 の元とするとき,
の元とするとき,
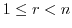 について,
について,
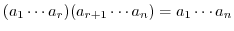
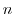 についての帰納法で証明する.
についての帰納法で証明する.
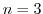 のときには,
のときには,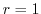 または
または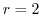 .したがって,
.したがって,
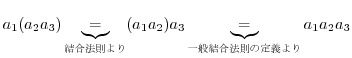
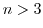 として,
として,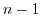 まで正しいと仮定すると
まで正しいと仮定すると
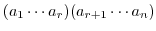 |
 |
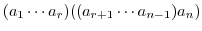 |
|
 |
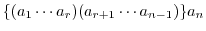 |
||
 |
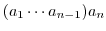 |
||
 |
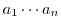 |
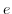 を群
を群 の単位元とするとき,
の単位元とするとき, の任意の元
の任意の元 と整数
と整数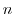 について
について
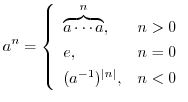
 の元
の元 と整数
と整数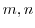 について,次の式が成り立つ.
について,次の式が成り立つ.
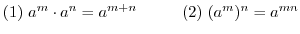
 の元
の元
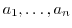 について,積
について,積
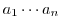 の逆元は次の式で与えられる.
の逆元は次の式で与えられる.
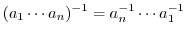
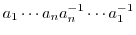 |
 |
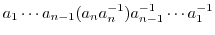 |
|
 |
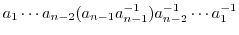 |
||
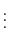 |
|||
 |
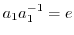 |
 の全ての元
の全ての元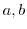 について次のことが成立するならば,
について次のことが成立するならば, は可換群であることを示せ.
は可換群であることを示せ.
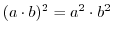
 が可換群のとき,
が可換群のとき, の元
の元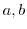 について,次のことが成立する.
について,次のことが成立する.
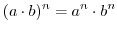
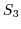 の元
の元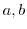 で,
で,
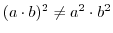 満たすものを1組あげよ.
満たすものを1組あげよ.
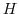 を群
を群 の部分群とする.
の部分群とする. の元
の元 に対して,
に対して,
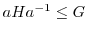 であることを示せ.ただし,
であることを示せ.ただし,
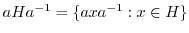 とする.
とする.
 を可換群,
を可換群,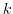 を正の整数とするとき,
を正の整数とするとき,
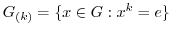 は
は の部分群であることを示せ.
の部分群であることを示せ.
 を可換群,
を可換群,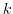 を正の整数とするとき,
を正の整数とするとき,
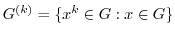 は
は の部分群であることを示せ.
の部分群であることを示せ.
 が次のような群のとき,それぞれの場合に,
が次のような群のとき,それぞれの場合に,
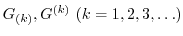 を求めよ.
を求めよ.
 を加法群
を加法群
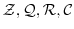 とするとき
とするとき
 をKleinの4元群
をKleinの4元群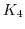 とするとき
とするとき