Next: 一般結合法則 Up: 群 Previous: クライン4元群 目次 索引
 の部分集合
の部分集合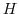 が
が の演算に関して群になっているとき,
の演算に関して群になっているとき,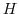 を
を の部分群(subgroup)といい,
の部分群(subgroup)といい,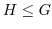 と表す.
と表す.
 の空でない部分集合を
の空でない部分集合を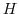 とする.
とする.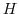 が
が の部分群であるための必要十分条件は,
の部分群であるための必要十分条件は,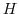 が次の条件(1)と(2)を満足していることである.
が次の条件(1)と(2)を満足していることである.

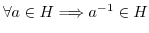
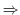 )
) 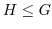 とすると,
とすると, の演算が
の演算が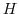 の演算でもあるから,
の演算でもあるから,
 となる.また,
となる.また,
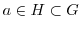 より,
より,
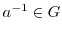 .ここで,
.ここで,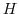 の単位元を
の単位元を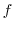 ,
, の単位元を
の単位元を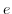 とすると,
とすると,
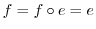 .したがって,
.したがって, の逆元を
の逆元を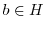 とすると,
とすると,
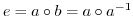 となり,
となり, の消去律より,
の消去律より,
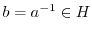 .
.
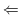 ) (1)より,
) (1)より,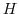 は演算に関して閉じている.また,
は演算に関して閉じている.また,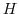 は
は の部分集合であるから,結合律は
の部分集合であるから,結合律は の結合律を継承する.ここで,
の結合律を継承する.ここで,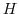 が群になるには,単位元と逆元の存在を示せばよいが,逆元はすでに(2)で示されている.そこで,単位元の存在について示す.
が群になるには,単位元と逆元の存在を示せばよいが,逆元はすでに(2)で示されている.そこで,単位元の存在について示す.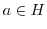 とすると,(2)より,
とすると,(2)より,
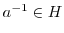 .また,(1)より
.また,(1)より
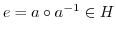 .
注 (1),(2)は次の(3)と同値である.
.
注 (1),(2)は次の(3)と同値である.
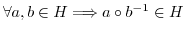
証明.
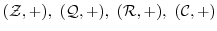 について,部分群の関係を調べよ.
について,部分群の関係を調べよ.
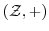 において,
において,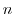 を正の整数とするとき,
を正の整数とするとき,
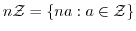 なる集合は
なる集合は
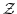 の部分群か調べよ.
の部分群か調べよ.
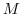 を第1行,第1列以外はすべて0である
を第1行,第1列以外はすべて0である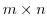 型行列とする.
型行列とする.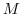 は
は
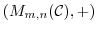 の部分群か調べよ.
の部分群か調べよ.
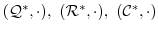 について,
について,
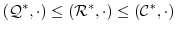
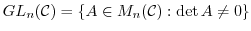
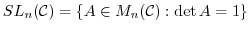
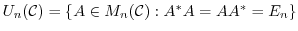
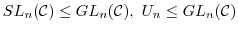 であることを示せ.
であることを示せ.
 を群とする.
を群とする.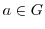 に対して,
に対して,
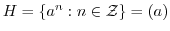 ,
,
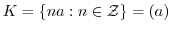 とすると,
とすると,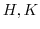 は
は の部分群であることを示せ.
の部分群であることを示せ.
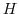 を群
を群 の部分群とし,
の部分群とし, を
を の任意の元として
の任意の元として
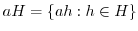 ,
,
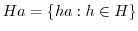 とおく.このとき,次のことが成り立つことを示せ.
とおく.このとき,次のことが成り立つことを示せ.
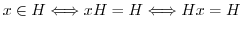
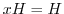 を示す.まず,
を示す.まず,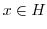 ならば,
ならば,
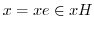 より,
より,
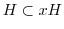 .次に,
.次に,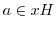 とすると,
とすると,
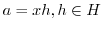 より,
より,
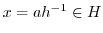 .したがって,
.したがって,
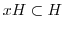 より,
より,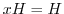 .
.
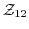 の部分集合
の部分集合
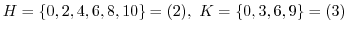
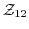 部分群である.このとき,
部分群である.このとき,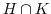 ,
,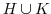 は部分群か調べよ.
は部分群か調べよ.
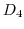 の部分集合
の部分集合
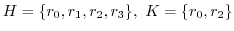
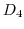 の部分群である.このとき,
の部分群である.このとき,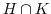 ,
, 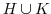 は部分群か調べよ.
は部分群か調べよ.
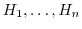 を
を の部分群とするとき,
の部分群とするとき,
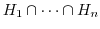 も
も の部分群である.
の部分群である.
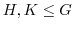 のとき,
のとき,
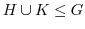 となるのはどんなときか.
となるのはどんなときか.