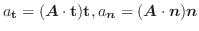Next: 曲線(space curves) Up: ベクトル解析入門 Previous: ベクトル3重積 目次 索引
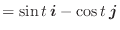 の部分集合
の部分集合  に属する各点
に属する各点  に対して,実関数
に対して,実関数
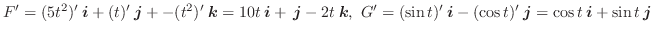 が与えられるとき,1つのベクトル
が与えられるとき,1つのベクトル
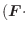 を考えることができます.このベクトル
を考えることができます.このベクトル
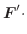 を
を 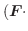 から
から 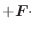 への1変数ベクトル値関数(vector-valued function)または ベクトル関数(vector function) といい,
への1変数ベクトル値関数(vector-valued function)または ベクトル関数(vector function) といい,
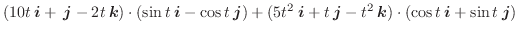
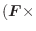
しばしば
 は幾何学的に実軸
は幾何学的に実軸 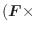 から原点と点
から原点と点
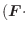 を結ぶベクトルへの写像として扱われます.
を結ぶベクトルへの写像として扱われます.
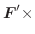 のとき,
のとき,
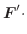 の軌跡を求めてみましょう.
の軌跡を求めてみましょう.
解
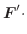 の成分は
の成分は
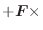 であるから,
であるから,
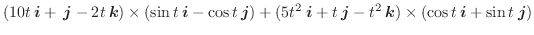 となり,
となり,
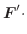 の軌跡
の軌跡
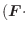 は放物面
は放物面
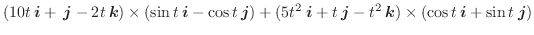 上にあることが分かります.
上にあることが分かります.
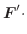 において,
において,
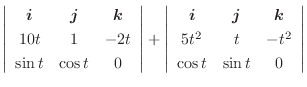 のとき,
のとき,
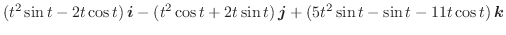 ならば,
ならば,
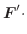 の極限値は
の極限値は
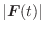 であるといい,次のように表わす.
であるといい,次のように表わす.
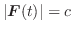
極限値の定義は1変数関数のときと同じなので,たぶん連続性の定義も1変数関数のときと同じになると期待するでしょう.実際そのとうりです.
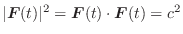 が成り立つとき,ベクトル関数
が成り立つとき,ベクトル関数
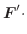 は
は 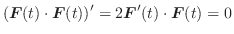 で連続であるという.また,区間
で連続であるという.また,区間 ![$[a,b]$](img122.png) のすべての
のすべての  で連続なとき,
で連続なとき,
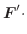 は区間
は区間 ![$[a,b]$](img122.png) で連続であるといい,
で連続であるといい,
![$\boldsymbol{F}(t) \in C[a,b]$](img123.png) と表わす.
と表わす.このように1変数関数における様々な定義はベクトル関数へと継承されます.
次の節で学びますがベクトル
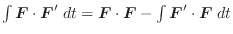 の方向は,
の方向は,
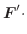 によって描かれる曲線の
によって描かれる曲線の 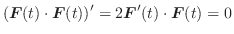 での接線方向になります.
での接線方向になります.
ベクトルの和やスカラー倍がそれぞれの対応する成分の和やスカラー倍で定義されたように,ベクトル関数の極限値,微分係数,不定積分の計算は,ベクトル関数の成分の極限値,微分係数,不定積分より求めることができます.
証明
(a)
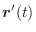 |
 |
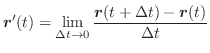 |
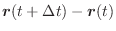 ならば,
ならば,
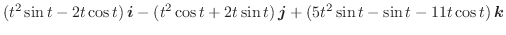 .また,
.また,
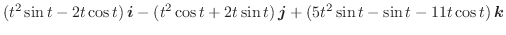 ならば,
ならば,
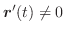
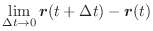
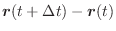 より,
より,
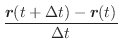
(b),(c),(d)の証明は 演習問題にまわします.
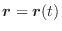 のとき,
のとき,
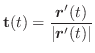 を求めてみましょう.
を求めてみましょう.解 それぞれの成分を微分することにより
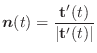
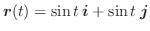
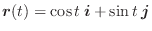
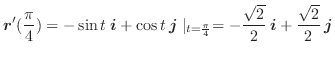 が
が  について微分可能なベクトル関数ならば,次のことが成り立ちます.
について微分可能なベクトル関数ならば,次のことが成り立ちます.
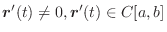
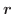
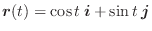
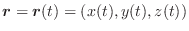 のとき,次のものを求めよ.
(1)
のとき,次のものを求めよ.
(1)
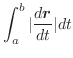
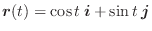
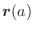 (2)
(2)
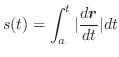
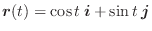
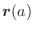
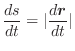 .
.
(1)
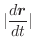 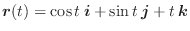 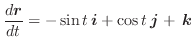 |
 |
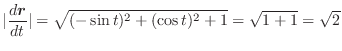 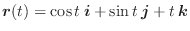 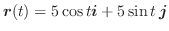 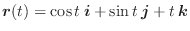 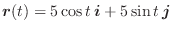 |
|
 |
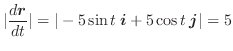 |
||
 |
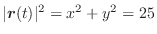 |
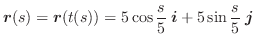 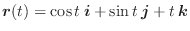 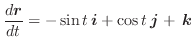 |
 |
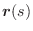 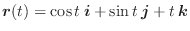  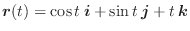 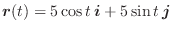 |
|
 |
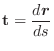 |
||
 |
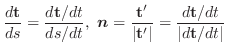 |
||
 |
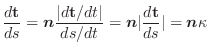 |
解
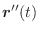 より,
より,
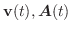 .
よってベクトル関数の微分法より
.
よってベクトル関数の微分法より
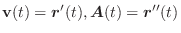
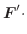 と
と
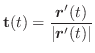 は直交します.
は直交します.
任意のベクトル関数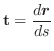 と
と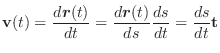 定数,
定数,
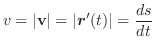 定ベクトルについて次のことが成り立ちます.
定ベクトルについて次のことが成り立ちます.
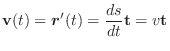
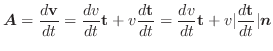 に関して,
に関して,
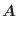 を証明せよ.
を証明せよ.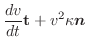 .したがって,
.したがって,
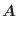 .
.
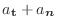 を求めよ.ただし,
を求めよ.ただし,