Next: 相関表,回帰直線(correlation table, regression line) Up: 資料の整理 Previous: 度数分布表(Frequency Tabulations) 目次 索引
散布度(dispersion)
5点満点のテストを行なったところ次のような度数分布表を得ました.
| 階級 | 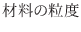 |
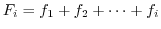 |
 |
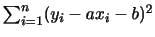 |
| 0 | 2 | 0.02 | 2 | 0.02 |
| 1 | 13 | 0.13 | 15 | 0.15 |
| 2 | 33 | 0.33 | 48 | 0.48 |
| 3 | 35 | 0.35 | 83 | 0.83 |
| 4 | 16 | 0.16 | 99 | 0.99 |
| 5 | 1 | 0.01 | 100 | 1.00 |
| 標本数 | 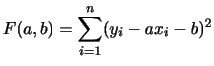 |
 |
 |
 |
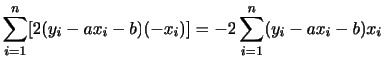 |
| 100 | 253 | 2.53 | 741 | 1.01 | 1.00 |
この表の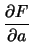 と
と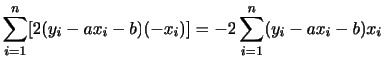 について説明します.
について説明します.
散布度 : データが平均のまわりに集中して分布するか,平均のまわりから散らばって分布するかの程度を表わすのが,散布度です.
度数分布表において,各階級数
 に対する度数を
に対する度数を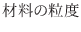 とするとき,変量
とするとき,変量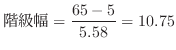 の平均
の平均
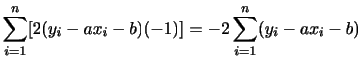 からの偏差の平方の平均:
からの偏差の平方の平均:
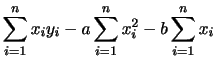 |
 |
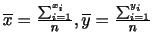 |
|
 |
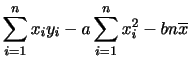 |
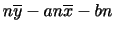
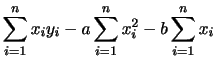 |
 |
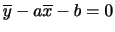 |
|
 |
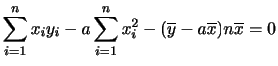 |
実際の問題では階級に分ける前にすべてのデータを打ち込むので,変量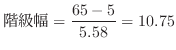 に関する
に関する 個のデータ
個のデータ
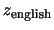 が与えられたとき,分散は次の式で与えられます.
が与えられたとき,分散は次の式で与えられます.
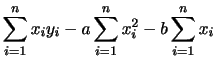 |
 |
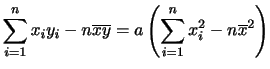 |
|
 |
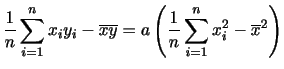 |
ここで分散を簡単に計算する実用的な方法として次の簡便計算法があります.
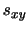
上の式を導きなさい.
解答
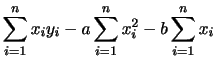 |
 |
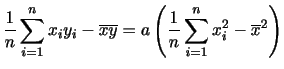 |
|
 |
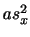 |
||
 |
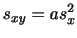 |
||
 |
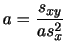 |
||
 |
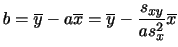 |
標準偏差は平均値のまわりのデータの散らばりの大きさを表す量ですが,標準偏差が10点であるといっても平均点が30点のときと,60点のときでは違いがあることが分かります.この違いを表す量として,変動係数とよばれるものがあります.変動係数はデータの平均値
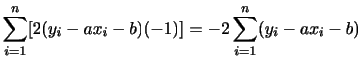 で標準偏差
で標準偏差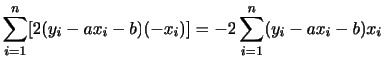 を割った割合
を割った割合
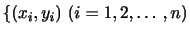 で表します.したがって,変動係数は平均値に対する相対的な散らばりの大きさを表します.
で表します.したがって,変動係数は平均値に対する相対的な散らばりの大きさを表します.
あるクラスの英語の試験の平均点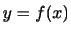 は
は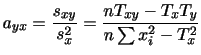 で標準偏差
で標準偏差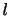 は
は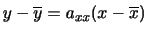 .また,数学の試験の平均点
.また,数学の試験の平均点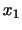 は
は で標準偏差
で標準偏差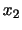 は
は でした.このクラスのA君の成績は英語が75点で数学が68点でした.A君のクラスでの成績は,英語と数学のどちらの順位が上でしょうか.
でした.このクラスのA君の成績は英語が75点で数学が68点でした.A君のクラスでの成績は,英語と数学のどちらの順位が上でしょうか.
解答 2つの異なるものを比較するには,共に同じ土俵にもってこなくてはなりません.その方法として標準化とよばれるものがあります.
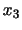
 の平均は0に分散
の平均は0に分散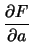 は1になります.そこで,英語の成績と数学の成績の標準化を行うと,
は1になります.そこで,英語の成績と数学の成績の標準化を行うと,
 |
 |
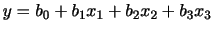 |
|
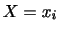 |
 |
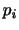 |
相関関係
2次元データの分布の特徴は2つの変数の平均値と分散だけでは表わすことが困難です.そこで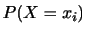 の
の 組のデータを
組のデータを
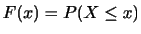
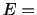
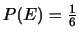
 は変量
は変量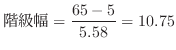 の標準偏差,
の標準偏差, は変量
は変量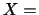 の標準偏差を表わします.
の標準偏差を表わします.
|
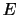 であるような標本値
であるような標本値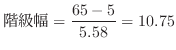 をpパーセント点といいます.特に,25%点
をpパーセント点といいます.特に,25%点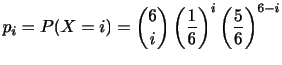 を第1四分位数, 50%点
を第1四分位数, 50%点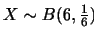 を第2四分位数, 75%点
を第2四分位数, 75%点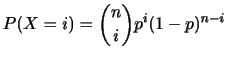 を第3四分位数といいます.次の20個のデータの第1四分位数を求めよ.
を第3四分位数といいます.次の20個のデータの第1四分位数を求めよ.
| 67 | 54 | 54 | 66 | 56 | 65 | 46 | 35 | 45 | 45 |
| 83 | 72 | 54 | 58 | 47 | 60 | 43 | 82 | 76 | 92 |
|