Next: 検定に用いる統計量(test statistics) Up: 統計的検定 Previous: 比率の検定(proportion test) 目次 索引
 が対応しています.
が対応しています.
(1) 多項分布に対する適合度の検定
ある試行の結果,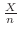 個の事象
個の事象
 のいずれかが現われるとします.ここで,
のいずれかが現われるとします.ここで, が起こる確率を
が起こる確率を とすると,
とすると,
 |
 |
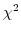 |
|
 |
 |
 |
 回独立に行なうとき,
回独立に行なうとき,
 がそれぞれ
がそれぞれ
 回現われる確率は
回現われる確率は

 のときは,2項分布に他なりません.この2項分布の一般化を多項分布(multinomial distribution)といい,
のときは,2項分布に他なりません.この2項分布の一般化を多項分布(multinomial distribution)といい, 回の独立試行で事象
回の独立試行で事象 が起こる回数を確率変数
が起こる回数を確率変数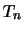 で表すと,
で表すと,

それぞれの目が出る確率が等しいサイコロがある.これを6回投げたとき,1から6までが1回ずつ現れる確率を求めよ.
解 各数字が現れる確率は
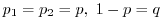 で,1から6までが1回ずつ現れる組み合わせは
で,1から6までが1回ずつ現れる組み合わせは
 通り.したがって,その確率は
通り.したがって,その確率は

次に,
 の互いに排反な事象のいずれかが現われる多項分布を考えます.
の互いに排反な事象のいずれかが現われる多項分布を考えます.
 とすると,大きさ
とすると,大きさ の標本のうち
の標本のうち に入る期待値は
に入る期待値は
 となります.一方,大きさ
となります.一方,大きさ の標本のうち
の標本のうち の部分に入る個数を確率変数
の部分に入る個数を確率変数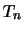 で表すと,次のことが知られています.
で表すと,次のことが知られています. のとき,
のとき,

 に従う.
に従う.
理論度数 と実測度数
と実測度数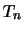 がすべての
がすべての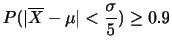 について近い値であれば,
について近い値であれば,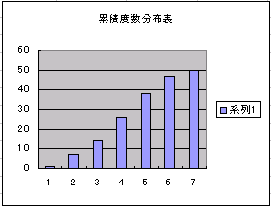 は全体として小さな値となります.したがって,
は全体として小さな値となります.したがって, が大きな値となったとき,その理論値
が大きな値となったとき,その理論値 に疑問が持たれます.このことから,次のような適合度の検定が得られます.
帰無仮説
に疑問が持たれます.このことから,次のような適合度の検定が得られます.
帰無仮説

( は正数で
は正数で
 となる数)
となる数)
対立仮説

ただし,
 である.
ここでは問題の性質上,片側検定にあたるものは考えられません.
である.
ここでは問題の性質上,片側検定にあたるものは考えられません.
 のもとで
のもとで に入る理論度数
に入る理論度数 は,
は,

 は十分大きな値で,すべての
は十分大きな値で,すべての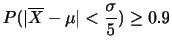 に対して
に対して
 となるとします.
となるとします. に入る標本値が
に入る標本値が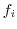 であるとき
であるとき
 ならば
ならば を棄却する.
を棄却する.
これによって適合度が検定できます.
あるサイコロを600回投げたところ,次のような表が得られた.各目の現れる確率が等しいと考えられるか,有意水準0.05で検定しよう.
| 目の数 | 1 | 2 | 3 | 4 | 5 | 6 | 計 |
| 回数 | 102 | 89 | 87 | 106 | 115 | 101 | 600 |
解
1
 : 「各目の現れる確率は等しい」
: 「各目の現れる確率は等しい」

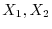 : 「各目の現れる確率は等しくない」
: 「各目の現れる確率は等しくない」

2 有意水準
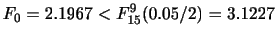
3 統計量

4  のもとで,
のもとで,
 |
 |
 |
|
 |
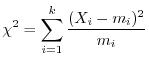 |
5
 より,
より,

 を容認.
を容認.
|
 のメンデル比に従って現われるとされているが,実験の結果次の表を得た.メンデル比に従っているといえるか,有意水準5%で検定しよう.
のメンデル比に従って現われるとされているが,実験の結果次の表を得た.メンデル比に従っているといえるか,有意水準5%で検定しよう.
| 遺伝形質 | A | B | C | D | 計 | |
| 観測度数 | 243 | 72 | 78 | 15 | 408 |
(2) 確率分布に対する適合度の検定
ここでは,ある分布が正規分布に従う,あるいはポワソン分布に従う,ということ自体が帰無仮説となる適合度検定を考えます.つまり,
帰無仮説  : 「ある分布Dに従う」
: 「ある分布Dに従う」
を設定します. の分布は既知であって,母数
の分布は既知であって,母数
 を含んでいるとします.例えば,正規分布では
を含んでいるとします.例えば,正規分布では
 の2個の母数を含み,これらの値は不明であるとします.
の2個の母数を含み,これらの値は不明であるとします.
次に排反な各階級
 に入る個数
に入る個数
 の実現値を
の実現値を
 とし,母数
とし,母数
 をこの値を用いて推定します.つまり,
をこの値を用いて推定します.つまり,

 を用いて各階級
を用いて各階級
 に入るべき期待度数
に入るべき期待度数
 を求めます.ここで,
を求めます.ここで,
 . つまり,
. つまり,

 であることが分かっています.そして,これを用いて
であることが分かっています.そして,これを用いて の検定を行ないます.
の検定を行ないます.
ある軍隊の10個の部隊において,1年間に馬に蹴られて死亡した兵士の数とその部隊数を10年間調べた結果次のような表になった.
| 死亡者数 | 0 | 1 | 2 | 3 | 4 | 計 |
| 部隊数 | 109 | 65 | 22 | 3 | 1 | 200 |
1
 : 「ポワソン分布
: 「ポワソン分布
 に従っている」
に従っている」
2 有意水準
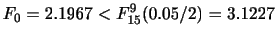
3 統計量
この表をポワソン分布とみて,死亡数の理論値を求める.これがポワソン分布
 によるものと考えて,
によるものと考えて, の値を推定する.死亡者数
の値を推定する.死亡者数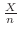 のときの確率を
のときの確率を とすると,
とすると,

| 死亡者数 | 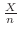 |
0 | 1 | 2 | 3 | 4 | 計 |
| 部隊数 | 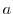 |
109 | 65 | 22 | 3 | 1 | 200 |
 |
0 | 65 | 44 | 9 | 4 | 122 | |
 |
0.5435 | 0.3313 | 0.1011 | 0.0206 | 0.0031 | ||
| 理論度数 |  |
108.7 | 66.3 | 20.2 | 4.1 | 0.6 |
 より
より
 .これより平均値
.これより平均値 は
は

| 死亡者数 | 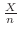 |
0 | 1 | 2 | 3 | 4 | 計 |
| 部隊数 | 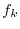 |
109 | 65 | 22 | 3 | 1 | 200 |
| 理論度数 |  |
108.7 | 66.3 | 20.2 | 4.1 | 0.6 |
この表で, の所の
の所の は単独で5よりも小さいので,
は単独で5よりも小さいので, 検定ができない.そこで,右から順に
検定ができない.そこで,右から順に を加えて5を越すまで合併すると,
を加えて5を越すまで合併すると, の階級を1つにしなければならない.したがって,
の階級を1つにしなければならない.したがって,

4  のもとで,
のもとで,
 |
 |
 |
|
 |
 |
5
 より,
より,

 を容認.
を容認.
母数 が標本から1個推定されたので,自由度は
が標本から1個推定されたので,自由度は
 となる.
となる.
(3) 独立性の検定
母集団の要素は,すべて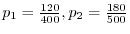 の2種類の属性をもち,
の2種類の属性をもち,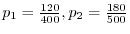 はそれぞれ排反な
はそれぞれ排反な
 および
および
 に分かれているとします.母集団から大きさ
に分かれているとします.母集団から大きさ の標本を抽出して,
の標本を抽出して,
 に入る観測度数を
に入る観測度数を とすると,次の表のように行列の形に整理できる.
とすると,次の表のように行列の形に整理できる.
 |
 |
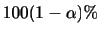 |
 |
和 | |
 |
 |
 |
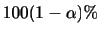 |
 |
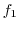 |
 |
 |
 |
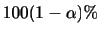 |
 |
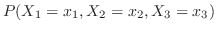 |
 |
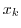 |
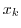 |
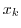 |
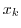 |
|
 |
 |
 |
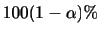 |
 |
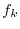 |
 は周辺度数である.このような表を
は周辺度数である.このような表を
 分割表(contingency table)という.
分割表(contingency table)という.
これを用いて,母集団の属性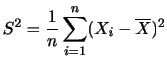 と
と が無関係であるかを調べることを独立性の検定という.独立性の検定には適合度の検定を応用することができる.
が無関係であるかを調べることを独立性の検定という.独立性の検定には適合度の検定を応用することができる.
対
 の出現度数の確率変数を
の出現度数の確率変数を ,
,
 の実現する確率を
の実現する確率を
 .また,
.また,
 が同時に起こる確率を
が同時に起こる確率を とする.
とする.
ここで,次のような適合度の検定を考える.
帰無仮説 : 「属性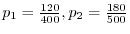 は独立である」
は独立である」
対立仮説 : 「属性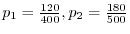 は従属である」
は従属である」
帰無仮説 のもとで
のもとで

 は母数なのでこれを最尤法によって推定すると,それらの推定値は
は母数なのでこれを最尤法によって推定すると,それらの推定値は

 が十分大きければ,帰無仮説
が十分大きければ,帰無仮説 のもとで統計量
のもとで統計量

 のカイ2乗分布に従うことが知られている.観測度数
のカイ2乗分布に従うことが知られている.観測度数 を用いると,統計量
を用いると,統計量 の実現値は
の実現値は
 |
 |
 |
|
 |
 |
|
| 死亡者数 | 0 | 1 | 2 | 3 | 4 | 計 |
| 部隊数 | 142 | 99 | 46 | 11 | 3 | 300 |
2 350人の大人を無作為に抽出して,飲酒と喫煙について答えてもらった.その際,飲酒の程度を低い方から
 と3段階に分け,喫煙の程度は低い方から
と3段階に分け,喫煙の程度は低い方から
 と4段階に分けた.結果は次の通りであった.飲酒と喫煙は関係があるか,有意水準5%で検定しよう.
と4段階に分けた.結果は次の通りであった.飲酒と喫煙は関係があるか,有意水準5%で検定しよう.
 |
 |
 |
 |
計 | ||
 |
39 | 54 | 49 | 17 | 159 | |
 |
27 | 43 | 40 | 9 | 119 | |
 |
14 | 23 | 15 | 20 | 72 | |
| 計 | 80 | 120 | 104 | 46 | 350 |