Next: 母比率の区間推定(大標本の場合)(confidence interval for population Up: 統計的推定法 Previous: 最尤推定(maximum likelihood estimation) 目次 索引
区間推定(interval estimation)
母数 がある区間
がある区間
![$[\theta_{1},\theta_{2}]$](img307.png) に入るだろうと推定するのが区間推定です.詳しくいうと,
母数
に入るだろうと推定するのが区間推定です.詳しくいうと,
母数 を推定するために,母集団から無作為に抽出された標本から2つの統計値
を推定するために,母集団から無作為に抽出された標本から2つの統計値
 を定める.このとき,あらかじめ指定された小さな確率
を定める.このとき,あらかじめ指定された小さな確率
 に対して,常に
に対して,常に
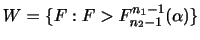
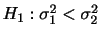 を
を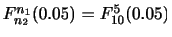 の信頼区間(Confidence interval),
の信頼区間(Confidence interval),
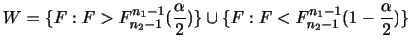 を信頼限界(Confidence limit),
を信頼限界(Confidence limit),
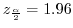 を信頼係数(Confidence coefficient)または信頼度(Confidence level)といいます.信頼区間
を信頼係数(Confidence coefficient)または信頼度(Confidence level)といいます.信頼区間
![$[\theta_{1},\theta_{2}]$](img307.png) を求めることを区間推定(Interval estimation)といいます.
を求めることを区間推定(Interval estimation)といいます.
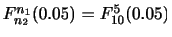 は一定値ですが,区間
は一定値ですが,区間
![$[\theta_{1},\theta_{2}]$](img307.png) は標本によっていろいろ変わり,この区間に
は標本によっていろいろ変わり,この区間に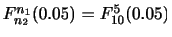 が入る確率が
が入る確率が
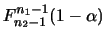 です.
です.
区間推定法(interval estimation method)
母集団が正規分布
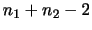 に従い,母分散
に従い,母分散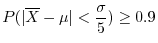 が分っているとします.このとき,母平均
が分っているとします.このとき,母平均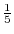 はどの範囲にあるかを,どのくらい信頼できるかを考えて表わしてみましょう.
はどの範囲にあるかを,どのくらい信頼できるかを考えて表わしてみましょう.
準備
標本
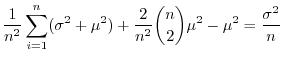 が,
が,
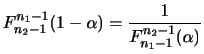 のとき,
のとき,
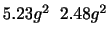
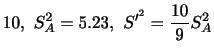
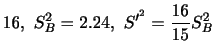 の期待値
の期待値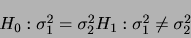
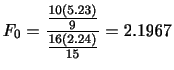 の期待値
の期待値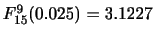
母平均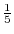 の区間推定(
の区間推定(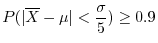 既知)
既知)
ここでは
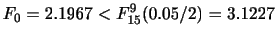 つまり,95%信頼区間を推定します.まず,
つまり,95%信頼区間を推定します.まず,
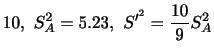
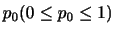
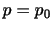
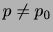 は,
は,
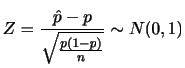
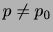 を標準正規分布表の両側確率で求めると,
を標準正規分布表の両側確率で求めると,
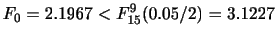 のとき,
のとき,
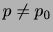 は
は
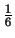
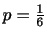
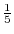 について解くと
について解くと
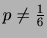
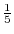 の信頼区間となります.
の信頼区間となります.
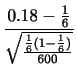 が与えられたとして,標準偏差が
が与えられたとして,標準偏差が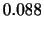 である正規母集団の平均に対する
である正規母集団の平均に対する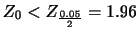 信頼区間を求めよう.
信頼区間を求めよう.
解答 標準偏差が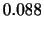 より,母分散
より,母分散
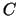 は既知である.この母集団から無作為に選んだ標本
は既知である.この母集団から無作為に選んだ標本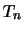 は
は
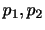 の正規分布に従っていると考えることができる.したがって,
の正規分布に従っていると考えることができる.したがって,
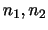
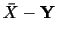 を求めると,
を求めると,
![$\displaystyle \bar{X} = \frac{1}{4}[145.3 + 145.1 + 145.4 + 146.2] = \frac{132}{4} = 145.25$](img336.png)
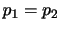
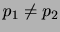 . また,
. また,
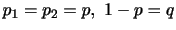 . したがって,
. したがって,
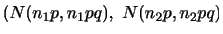
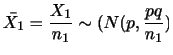
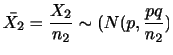
次に,母集団が正規分布に従うことは分かっているが母分散
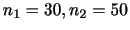 が不明である場合を考えます.
が不明である場合を考えます.
平均値の区間推定(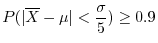 未知)
未知)
ここでは
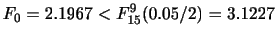 つまり,95%信頼区間を推定します.
この場合,2つの母数
つまり,95%信頼区間を推定します.
この場合,2つの母数
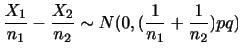 が必要となりますが,
が必要となりますが,
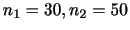 が未知なので,
が未知なので,
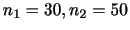 を推定する不偏分散
を推定する不偏分散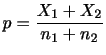 を
を
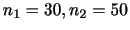 の代わりに用います.すると,母分散に無関係に
の代わりに用います.すると,母分散に無関係に
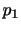
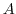 の
の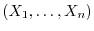 分布に従うことが知られています.これより,
分布に従うことが知られています.これより,
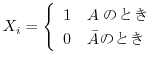
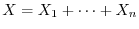 は,
は,
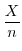
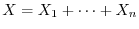 を
を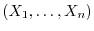 分布表の両側確率で求めると,
分布表の両側確率で求めると,
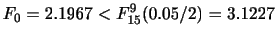 ,
,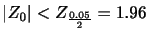 のとき,
のとき,
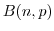 は
は
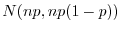
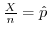
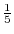 について解くと
について解くと
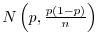
|
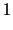 であることがわかっている.いま
であることがわかっている.いま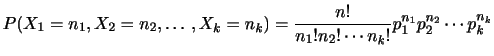 個の標本をとり,標本平均
個の標本をとり,標本平均
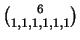 を得た.このとき信頼度
を得た.このとき信頼度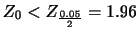 で,この水質の母平均の区間推定をせよ.
で,この水質の母平均の区間推定をせよ.
2 標本
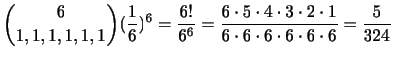 が与えられたとして,母平均が
が与えられたとして,母平均が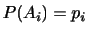 で標準偏差が
で標準偏差が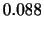 ある正規母集団の平均に対する
ある正規母集団の平均に対する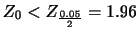 信頼区間を求めよう.
信頼区間を求めよう.
3 標本
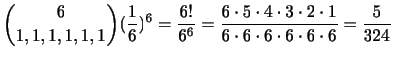 が与えられたとして,母平均が
が与えられたとして,母平均が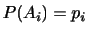 である正規母集団の平均に対する
である正規母集団の平均に対する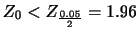 信頼区間を求めよう.
信頼区間を求めよう.