: 行列と行列式 : ベクトル空間 : 1次独立と1次従属目次索引

部分空間と次元

ベクトルの和とスカラー倍がベクトル空間の部分集合に用いられると, 新しいベクトル空間を作り出すことがあります．こうしてできたベクトル空間を部分空間といいます．つまり

定義 1.9 ベクトル空間

と空でない部分集合

が次の性質をもつとき,

は

の 部分空間(subspace)であるという．

${\bf w}_{1}, {\bf w}_{2}$ が

に含まれるならば, 和 ${\bf w}_{1} + {\bf w}_{2}$ もWに含まれる．

w がWに含まれるならば, スカラー倍 $\alpha {\bf w}$ もWに含まれる．

部分空間はそれ自身ベクトル空間です．つまりベクトル空間になるための1から9までの性質を満たしています．では, なぜ性質1と6しか調べなくてもベクトル空間になれるのかといいますと, 他の性質は親から受け継ぐので親がベクトル空間なら満たしているのです．部分空間を手っ取り早く作る方法に次のものがあります．

ベクトル ${\bf v}_{1},{\bf v}_{2}, {\bf v}_{3}, \ldots , {\bf v}_{n}$ の1次結合全体の集合を $\langle{\bf v}_{1},{\bf v}_{2}, {\bf v}_{3}, \ldots , {\bf v}_{n}\rangle$ で表し, ${\bf v}_{1},{\bf v}_{2}, {\bf v}_{3}, \ldots , {\bf v}_{n}$ で張られた部分空間(linear span) といいます．名前の通りこれは部分空間です．

例題 1.19 $\langle{\bf v}_{1},{\bf v}_{2}, {\bf v}_{3}, \ldots , {\bf v}_{n}\rangle$ はベクトル空間Vの部分空間であることを証明しよう．

解 ${\bf v},{\bf w}$ を $\langle{\bf v}_{1},{\bf v}_{2}, {\bf v}_{3}, \ldots , {\bf v}_{n}\rangle$ の元とすると,

$\displaystyle {\bf v}$	$\displaystyle =$	$\displaystyle c_{1}{\bf v}_{1} + c_{2}{\bf v}_{2} + c_{3}{\bf v}_{3} + \cdots + c_{n}{\bf v}_{n},$
$\displaystyle {\bf w}$	$\displaystyle =$	$\displaystyle d_{1}{\bf v}_{1} + d_{2}{\bf v}_{2} + d_{3}{\bf v}_{3} + \cdots + d_{n}{\bf v}_{n}.$

これより,

$\displaystyle {\bf v} + {\bf w} = (c_{1}+d_{1}){\bf v}_{1} + (c_{2}+d_{2}){\bf v}_{2} + \cdots + (c_{n}+d_{n}){\bf v}_{n},$

$\displaystyle \alpha {\bf v} = (\alpha c_{1}){\bf v}_{1} + (\alpha c_{2}){\bf v}_{2} + \cdots + (\alpha c_{n}){\bf v}_{n}.$

よって, v + w, $\alpha$ v ともに $\langle{\bf v}_{1},{\bf v}_{2}, {\bf v}_{3}, \ldots , {\bf v}_{n}\rangle$ に含まれる． $\blacksquare$

例題 1.20

は

の部分空間であることを示そう．

解 $f(x),g(x) \in C[a,b]$ ならば, $f(x) + g(x) \in C[a,b], \alpha f(x) \in C[a,b]$ である．なぜなら連続な関数の和はまた連続．連続な関数の定数倍もまた連続． $\blacksquare$

例題 1.21

をベクトル空間

の部分空間とするとき, その共通部分 $U \cap W$ と和集合

は, ともに

の部分空間になることを示そう．ただし

$\displaystyle U \cap W = \{{\bf v} : {\bf v} \in U$ かつ $\displaystyle {\bf v} \in W \},$

$\displaystyle U + W = \{{\bf u} + {\bf w} : {\bf u} \in U, {\bf w} \in W \}.$

解 ${\bf u},{\bf w} \in U \cap W$ とすると, ${\bf u},{\bf w} \in U$ かつ ${\bf u},{\bf w} \in W$ ．これより

$\displaystyle {\bf u} + {\bf w} \in U \cap W.$

また $\alpha {\bf u} \in U$ かつ $\alpha {\bf u} \in W$ より

$\displaystyle \alpha {\bf u} \in U \cap W.$

したがって, $U \cap W$ は

の部分空間である．

また ${\bf u},{\bf w} \in U + W$ とすると, ${\bf u} = {\bf u}_{1} + {\bf w}_{1}, {\bf w} = {\bf u}_{2} + {\bf w}_{2}$ . これより

$\displaystyle {\bf u} + {\bf w} = ({\bf u}_{1} + {\bf w}_{1} ) + ({\bf u}_{2} +... ...w}_{2} ) ({\bf u}_{1} + {\bf u}_{2} ) + ({\bf w}_{1} + {\bf w}_{2} )\in U + W,$

$\displaystyle \alpha {\bf u} = \alpha ({\bf u}_{1} + {\bf w}_{1}) = \alpha {\bf u}_{1} + \alpha {\bf w}_{1} \in U + W.$

よって,

は

の部分空間である． $\blacksquare$

において, とくにの任意の元 ${\bf w}$ が, ${\bf w} = {\bf u} + {\bf w} ({\bf u} \in U, {\bf w} \in W)$ の形に一意的に表されるとき, はとの 直和(direct sum) といい, $U \bigoplus W$ で表します．

$\spadesuit$ 基底 $\spadesuit$

定義 1.10 ベクトルの組 $\{{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{n}\}$ が次の性質をもつとき, ベクトル空間

の 基底(basis)であるという．
$(a) {\{{\bf v}_{i}\}}_{i=1}^{n}$ が互いに1次独立である．

のベクトル v が ${\{{\bf v}_{i}\}}_{i=1}^{n}$ の1次結合で表せる．つまり $V = \langle{\bf v}_{1},{\bf v}_{2}, \ldots , {\bf v}_{n}\rangle$ . このことを, ベクトル ${\{{\bf v}_{i}\}}_{i=1}^{n}$ は空間を張っているという．

明らかに1次独立なベクトルの組がみな基底になれるわけではありません．たとえば, 3次元ベクトル空間でのベクトルの組 $\{{\bf i},{\bf j}\}$ を考えてみましょう． $\{{\bf i},{\bf j}\}$ は1次独立ですがどんな実数 $c_{1},c_{2}$ を用いても ${\bf k} = c_{1}{\bf i} + c_{2}{\bf j}$ は不可能です．

$\{{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{n}\}$ の中で互いに1次独立であるものの最大個数をとします．また, それらを $\{{\bf v}_{1}, {\bf v}_{2}, \ldots, {\bf v}_{r}\}$ とすると, 残りのベクトル ${\bf v}_{r+1},\ldots,{\bf v}_{n}$ はそれぞれ

$\displaystyle \{{\bf v}_{1}, {\bf v}_{2}, \ldots, {\bf v}_{r}\}$

と1次従属です．よって, 定理1.3より $\{{\bf v}_{1}, {\bf v}_{2}, \ldots, {\bf v}_{r}\}$ の1次結合で表せます．したがって次のことがいえます．

$\spadesuit$ 次元 $\spadesuit$

定理 1.5 $V = \langle{\bf v}_{1},{\bf v}_{2}, \ldots , {\bf v}_{n}\rangle$ において, $\{{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{n}\}$ の中から互いに1次独立なベクトル $\{{\bf v}_{1}, {\bf v}_{2}, \ldots, {\bf v}_{r}\}$ をえらんで

$\displaystyle \langle{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{n}\rangle = \langle{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{r}\rangle$

とすることができる．このとき $\{{\bf v}_{1}, {\bf v}_{2}, \ldots, {\bf v}_{r}\}$ はこの部分空間の基底のひとつであり, この部分空間の 次元(dimension) は

であるといい, $\dim V = r$ と表す．

例題 1.22

を平面

上のベクトルの集まりとする．つまり,

$\displaystyle S = \{(x,y,-x-y) : x,y \in R\}．$

このとき,

の基底と次元を求めよう．

解まず $S = \{(x,y,-x-y) : x,y \in R\}$ はの部分空間であることを示す． ${\bf s}_{1},{\bf s}_{2}$ をの元とすると, ${\bf s}_{1} = (x_{1},y_{1},-x_{1}-y_{1}), {\bf s}_{2} = (x_{2},y_{2},-x_{2}-y_{2})$ と表せるので,

$\displaystyle {\bf s}_{1}+{\bf s}_{2} = (x_{1}+x_{2},y_{1}+y_{2},-(x_{1}+x_{2})-(y_{1}+y_{2})),$

$\displaystyle \alpha{\bf s}_{1} = \alpha(x_{1},y_{1},(-x_{1}-y_{1})) = (\alpha x_{1}, \alpha y_{1}, -\alpha x_{1}-\alpha y_{1}).$

よって,

は

の部分空間となる．次に, ${\bf s}$ を

の任意のベクトルとすると, ${\bf s} = (x,y,-x-y)$ . ${\bf i},{\bf j},{\bf k}$ を用いてsを表すと,

$\displaystyle {\bf s} = x{\bf i} + y{\bf j} -(x+y){\bf k} = x({\bf i} - {\bf k}) + y({\bf j} - {\bf k}).$

したがって,

に含まれるすべてのベクトルは, ${\bf i} - {\bf k}$ と ${\bf j} - {\bf k}$ の1次結合で表せる．また ${\bf i} - {\bf k}$ と ${\bf j} - {\bf k}$ は互いに1次独立なので, ${\bf i} - {\bf k}$ と ${\bf j} - {\bf k}$ は

の基底になる．よって $\dim S = 2$ . $\blacksquare$

次の節にうつる前に, 和空間と共通部分の次元について述べた次元公式とよばれる定理を学びましょう．証明は演習問題1.4を参照して下さい．

定理 1.6

をベクトル空間

の部分空間とするとき, 次の公式が成り立つ．

$\displaystyle \dim (U + W) = \dim U + \dim W - \dim(U \cap W).$

$\spadesuit$ Gram-Schmidtの直交化法 $\spadesuit$

1.2節で直交系から正規直交系を作り出すことを学びました．ここでは1次独立なベクトルから正規直交系を作り出すことを学びます．まず個のベクトル ${\bf v}_{1},{\bf v}_{2}, \ldots ,{\bf v}_{m}$ に対して

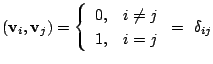
$\displaystyle ({\bf v}_{i},{\bf v}_{j}) = \left \{ \begin{array}{cl} 0,& i \neq j \\ 1,& i = j \end{array}\right. = \delta_{ij}$

が成り立つとき,

個のベクトルは正規直交系をなすといいます．ここで $\delta_{ij}$ は クロネッカーのデルタ(Kronecker delta) とよばれるものです．正規直交系の例を1.2節でいくつか見ましたがよく観察するとそれらはすべて1次独立です．これから次のような定理が生まれました．

定理 1.7 $\{{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{m}\}$ が正規直交系をなすとき, これらは1次独立である．

証明 $c_{1}{\bf v}_{1} + c_{2}{\bf v}_{2} + \cdots + c_{m}{\bf v}_{m} = {\bf0}$ とし, ${\bf v}_{1}$ との内積を作ると

$\displaystyle 0 = ({\bf v}_{1},{\bf0})$	$\displaystyle =$	$\displaystyle ({\bf v}_{1},c_{1}{\bf v}_{1} +c_{2}{\bf v}_{2} + \cdots + c_{m}{\bf v}_{m})$
	$\displaystyle =$	$\displaystyle ({\bf v}_{1},c_{1}v_{1}) + ({\bf v}_{1},c_{2}{\bf v}_{2}) + \cdots + ({\bf v}_{1},c_{m}{\bf v}_{m})$
	$\displaystyle =$	$\displaystyle c_{1}({\bf v}_{1},{\bf v}_{1})$
	$\displaystyle =$	$\displaystyle c_{1} .$

他の $c_{i}$ も同様にして 0 になるので $\{{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{m}\}$ は1次独立である． $\blacksquare$

この定理の逆, つまり, 1次独立なベクトルから正規直交系を作ることができるのか考えてみます．まず, ${\mathbf x}_{1}, {\mathbf x}_{2}, \ldots, {\mathbf x}_{m}$ が1次独立だとします．当然すべてのベクトル ${\mathbf x}_{i} \neq 0$ (なぜ?)．そこで $\displaystyle{\frac{{\mathbf x}_{1}}{\Vert{\mathbf x}_{1}\Vert} = {\bf v}_{1}}$ とすると, ${\bf v}_{1}$ は単位ベクトルになります．次に ${\bf v}_{1}$ と ${\mathbf x}_{2}$ の1次結合の中から ${\bf v}_{1}$ と直交するものを選び出します．幾何ベクトルでいえば, ${\bf v}_{1}$ と ${\mathbf x}_{2}$ の決定する平面の中に ${\bf v}_{1}$ と直交するベクトルを見つけることになります．そこで ${\bf w}_{2} = c_{1}{\bf v}_{1} + c_{2}{\mathbf x}_{2}$ を ${\bf v}_{1}$ と直交するベクトルとすると,

$\displaystyle ({\bf w}_{2},{\bf v}_{1})$	$\displaystyle =$	$\displaystyle (c_{1}{\bf v}_{1} + c_{2}{\mathbf x}_{2},{\bf v}_{1})$
	$\displaystyle =$	$\displaystyle c_{1} + c_{2}({\mathbf x}_{2},{\bf v}_{1})$
	$\displaystyle =$	$\displaystyle 0 .$

よって $c_{1} = -c_{2}({\mathbf x}_{2},{\bf v}_{1})$ . したがって,

$\displaystyle {\bf w}_{2} = c_{2}({\mathbf x}_{2} - ({\mathbf x}_{2},{\bf v}_{1}){\bf v}_{1})$

となります． ${\mathbf x}_{1},{\mathbf x}_{2}$ は1次独立なので ${\mathbf x}_{2} - ({\mathbf x}_{2},{\bf v}_{1}){\bf v}_{1} \neq {\bf0}$ . そこで

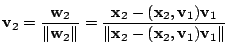
$\displaystyle {\bf v}_{2} = \frac{{\bf w}_{2}}{\Vert{\bf w}_{2}\Vert} = \frac{{... ... v}_{1}}{\Vert{\mathbf x}_{2} - ({\mathbf x}_{2},{\bf v}_{1}){\bf v}_{1}\Vert}$

とおくと ${\bf v}_{1} \perp {\bf v}_{2}, \Vert{\bf v}_{1}\Vert = \Vert{\bf v}_{2}\Vert = 1$ となります．

次に ${\bf v}_{1}$ と ${\bf v}_{2}$ に直交する単位ベクトル ${\bf v}_{3}$ を求めます．まず ${\bf v}_{1}, {\bf v}_{2}$ と ${\mathbf x}_{3}$ の1次結合 ${\bf w}_{3} = d_{1}{\bf v}_{1} + d_{2}{\bf v}_{2} + d_{3}{\mathbf x}_{3}$ を考えます．

$\displaystyle ({\bf w}_{3},{\bf v}_{1}) = ({\bf w}_{3},{\bf v}_{2}) = 0$

から

$\displaystyle d_{1} + d_{3}({\mathbf x}_{3},{\bf v}_{1}) = 0, d_{2} + d_{3}({\mathbf x}_{3},{\bf v}_{2}) = 0.$

ゆえに

$\displaystyle {\bf w}_{3} = d_{3}({\mathbf x}_{3} - ({\mathbf x}_{3},{\bf v}_{1}){\bf v}_{1} - ({\mathbf x}_{3},{\bf v}_{2}){\bf v}_{2}).$

${\mathbf x}_{1},{\mathbf x}_{2}, {\mathbf x}_{3}$ はもともと1次独立なので

$\displaystyle {\mathbf x}_{3} - ({\mathbf x}_{3},{\bf v}_{1}){\bf v}_{1} - ({\mathbf x}_{3},{\bf v}_{2}){\bf v}_{2} \neq {\bf0}.$

そこで

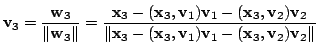
$\displaystyle {\bf v}_{3} = \frac{{\bf w}_{3}}{\Vert{\bf w}_{3}\Vert} = \frac{{... ...}_{3},{\bf v}_{1}){\bf v}_{1} - ({\mathbf x}_{3},{\bf v}_{2}){\bf v}_{2}\Vert}$

とおけば ${\bf v}_{1}$ と ${\bf v}_{2}$ に直交する単位ベクトルが得られます．以下同様にして,

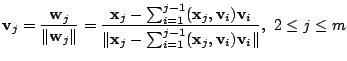
$\displaystyle {\bf v}_{j} = \frac{{\bf w}_{j}}{\Vert{\bf w}_{j}\Vert} = \frac{{... ...m_{i=1}^{j-1}({\mathbf x}_{j},{\bf v}_{i}){\bf v}_{i}\Vert}, 2 \leq j \leq m$

とすれば $\{{\bf v}_{1},{\bf v}_{2},\ldots,{\bf v}_{m}\}$ は正規直交系をなします．これを グラム・シュミットの直交化法(Gram-Schmidt orthogonalization) といいます．

例題 1.23

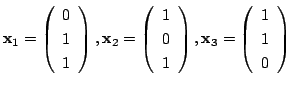
$\displaystyle {\mathbf x}_{1} = \left(\begin{array}{c} 0 \\ 1 \\ 1 \end{array... ...t ), {\mathbf x}_{3} = \left(\begin{array}{c} 1 \\ 1 \\ 0 \end{array}\right )$

から正規直交系を作ろう．

解

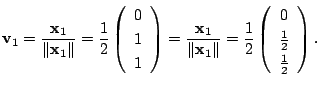
$\displaystyle {\bf v}_{1} = \frac{{\mathbf x}_{1}}{\Vert{\mathbf x}_{1}\Vert} =... ...\left(\begin{array}{c} 0 \\ \frac{1}{2} \\ \frac{1}{2} \end{array}\right ) .$

次に,

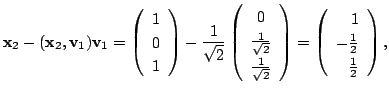
$\displaystyle {\mathbf x}_{2} - ({\mathbf x}_{2},{\bf v}_{1}){\bf v}_{1} = \lef... ...\left(\begin{array}{r} 1 \\ -\frac{1}{2} \\ \frac{1}{2} \end{array}\right ),$

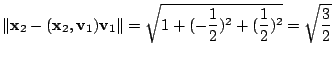
$\displaystyle \Vert{\mathbf x}_{2} - ({\mathbf x}_{2},{\bf v}_{1}){\bf v}_{1}\Vert = \sqrt{1 + (-\frac{1}{2})^2 + (\frac{1}{2})^2} = \sqrt{\frac{3}{2}}$

より

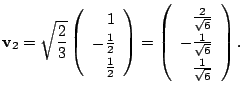
$\displaystyle {\bf v}_{2} = \sqrt{\frac{2}{3}}\left(\begin{array}{r} 1\\ -\fra... ...{\sqrt{6}} \\ -\frac{1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{array}\right ).$

最後に

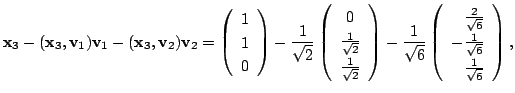
$\displaystyle {\mathbf x}_{3} - ({\mathbf x}_{3},{\bf v}_{1}){\bf v}_{1} - ({\m... ...2}{\sqrt{6}}\\ -\frac{1}{\sqrt{6}}\\ \frac{1}{\sqrt{6}} \end{array}\right ),$

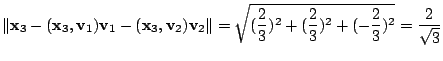
$\displaystyle \Vert{\mathbf x}_{3} - ({\mathbf x}_{3},{\bf v}_{1}){\bf v}_{1} -... ...qrt{(\frac{2}{3})^2 + (\frac{2}{3})^2 + (-\frac{2}{3})^2} = \frac{2}{\sqrt{3}}$

より

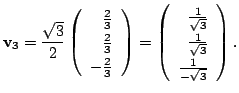
$\displaystyle {\bf v}_{3} = \frac{\sqrt{3}}{2}\left(\begin{array}{r} \frac{2}{3... ...}{\sqrt{3}}\\ \frac{1}{\sqrt{3}}\\ \frac{1}{-\sqrt{3}} \end{array}\right ) .$