next up previous contents index
: 行列の変換と固有値 : 線形写像 : 線形写像   目次   索引

線形写像

$ \spadesuit$写像 $ \spadesuit$

第1章, 第2章でベクトル空間について学んできました．この章では写像を用いてふたつのベクトル空間の関係を調べます．そこで写像について簡単に復習をしておきます．

ふたつの集合VとWを考えます．Vの任意の要素$ v$ に対してWのただひとつの要素$ w$ を対応させるような規則$ T$ があるとき, この対応関係$ T$ をVからWへの 写像(mapping) といい記号 $ T : V \longrightarrow W$ で表します．この考え方を用いると $ m \times n$型の行列は $ n$項列ベクトルを $ m$項列ベクトルに移す写像, 言い換えると, $ {\mathcal R}^{n}$ から $ {\mathcal R}^{m}$ への写像ということになります．

$ \spadesuit$線形写像 $ \spadesuit$

ベクトル空間には和とスカラー倍が定義されていました．そこで, ふたつのベクトル空間の関係を調べるのに使う写像は, 和とスカラー倍を保つのが望ましいでしょう．そのような写像を線形写像といい次のように定義します．

定義 3.1   $ V,W$ がベクトル空間のとき, 写像 $ T : V \longrightarrow W$ で次の条件を満たすものを 線形写像(linear mapping) という．
$ 1. T({\bf v} + {\bf w}) = T({\bf v}) + T({\bf w}) ({\bf v},{\bf w} \in V)$
$ 2. T(\alpha {\bf v}) = \alpha T({\bf v}) ({\bf v} \in V, \alpha \in R)$
とくに $ V = W$ のとき, $ T$ を $ V$ の 線形変換(linear transformation) という．

線形写像は $ V$ から $ W$ への写像のうちベクトル空間の性質を保つ写像です．$ T$ により $ V$ の移る先全体を $ T$ の 像(image) といい,

$\displaystyle Im (T) = T(V) = \{{\bf w} \in W : T({\bf v}) = {\bf w}を満たす{\bf v} \in Vが存在する\} $

で表します．また$ T$ による像が $ {\bf0}$ になるような$ V$ の要素の集まりを $ T$ の 核(kernal) といい,

$\displaystyle \ker (T) = \{{\bf v} \in V : T({\bf v}) = 0 \} $

で表します．これらは線形写像の性質より, それぞれ$ W,V$ の部分空間になることがわかります(演習問題3.1参照)．

例題 3.1   $ A$ を $ m \times n$型の行列とする．

$\displaystyle T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{m} $

を $ T({\mathbf x}) = A{\mathbf x}$ で定義すると $ T$ は線形写像になることを示そう．

解 行列どうしの積および実数との積の性質から, $ {\mathcal R}^{n}$ の任意のベクトル $ {\mathbf x}_{1},{\mathbf x}_{2}$および任意の実数 $ \alpha$ に対して,

$\displaystyle T({\mathbf x}_{1} + {\mathbf x}_{2}) = A({\mathbf x}_{1} + {\math... ...mathbf x}_{1}) + A({\mathbf x}_{2}) = T({\mathbf x}_{1}) + T({\mathbf x}_{2}), $

$\displaystyle T(\alpha {\mathbf x}_{1}) = A(\alpha {\mathbf x}_{1}) = \alpha A({\mathbf x}_{1}) = \alpha T({\mathbf x}_{1}) $

が成り立つ．よって $ T$ は線形写像である． $ \blacksquare$

線形写像 $ T : V \longrightarrow W$ が

$\displaystyle {\bf v}_{1} \neq {\bf v}_{2} $   ならば$\displaystyle T({\bf v}_{1}) \neq T({\bf v}_{2}) ({\bf v}_{1},{\bf v}_{2} \in V) $

を満たすとき, $ T$ は 1対1(one-to-one)であるといい, このような写像を 単射(injective) といいます．

線形写像 $ T : V \longrightarrow W$ が $ Im(T) = W$ を満たすとき, $ T$ を $ V$ から $ W$ の 上への(onto)線形写像といい, このような写像を 全射(surjective) といいます．

例題 3.2   $ S : U \longrightarrow V, T : V \longrightarrow W$ がともに線形写像であるとき, 合成写像 $ T \circ S : U \longrightarrow W$も線形写像であることを示そう．

解

$\displaystyle (T \circ S)(\alpha{\bf u}_{1} + \beta{\bf u}_{2})$ $\displaystyle =$ $\displaystyle T(S(\alpha{\bf u}_{1} + \beta{\bf u}_{2}))$  
  $\displaystyle =$ $\displaystyle T(\alpha S({\bf u}_{1}) + \beta S({\bf u}_{2}))$  
  $\displaystyle =$ $\displaystyle \alpha (T \circ S)({\bf u}_{1}) + \beta (T \circ S)({\bf u}_{2})$  

より合成写像 $ T \circ S : U \longrightarrow W$も線形写像． $ \blacksquare$

$ \spadesuit$同型写像 $ \spadesuit$

ベクトル空間からベクトル空間の上への1対1の線形写像をとくに同型写像(isomorphism) といいます．また, $ V$ から $ W$ への同型写像が存在するとき, $ V$ と $ W$ は 同型(isomorphic)であるといい, $ V \sim W$ と表します．また $ T : V \longrightarrow W$ が同型写像で, $ T({\bf v}) = {\bf w}$ のとき, $ S({\bf w}) = {\bf v}$ と定めることにより, $ W$ から $ V$ への写像$ S$ を得ます．このとき, $ S$ を $ T$ の 逆写像(inverse mapping) といい, $ S = T^{-1}$ と表します．ここで同型写像について次のことが成り立ちます．

定理 3.1   線形写像 $ T : V \longrightarrow {\mathcal R}^{n}$ について次の条件は同値である．
$ (1)$ $ \dim V = n$
$ (2)$ $ T$ は同型写像である．つまり $ V \sim {\mathcal R}^{n}$
$ (3)$ $ \ker(T) = \{{\bf0}\}, Im(T) = {\mathcal R}^{n}$
$ (4)$ 逆写像 $ T^{-1} : {\mathcal R}^{n} \longrightarrow V$ は同型写像である．
$ (5)$ $ \{{\bf w}_{1},{\bf w}_{2}, \ldots , {\bf w}_{n}\}$ が $ {\mathcal R}^{n}$ の基底ならば, 逆写像$ T^{-1}$ による像の集合

$ \{T^{-1}({\bf w}_{1}),T^{-1}({\bf w}_{2}), \ldots , T^{-1}({\bf w}_{n})\}$ は $ V$ の基底となる．

証明 $ (1) \Rightarrow (2)$
$ V$ の1組の基底を $ \{{\bf v}_{1},{\bf v}_{2}\ldots,{\bf v}_{n}\}$ とし, $ \{{\bf w}_{1},{\bf w}_{2}, \ldots , {\bf w}_{n}\}$ を $ {\mathcal R}^{n}$ の基底とする．ここで $ T : V \longrightarrow {\mathcal R}^{n}$ を $ T(\alpha_{1}{\bf v}_{1} + \alpha_{2}{\bf v}_{2} + \cdots + \alpha_{n}{\bf v}_{... ... \alpha_{1}{\bf w}_{1} + \alpha_{2}{\bf w}_{2} + \cdots + \alpha_{n}{\bf w}_{n}$ と定義すると, $ T$ は線形写像となる(演習問題3.1)．また $ {\bf a},{\bf b} \in V$ とすると, ある $ c_{1},c_{2},\ldots,c_{n}, d_{1},d_{2},\ldots,d_{n} \in R$ で

$\displaystyle {\bf a} = c_{1}{\bf v}_{1} + \cdots + c_{n}{\bf v}_{n}, $

$\displaystyle {\bf b} = d_{1}{\bf v}_{1} + \cdots + d_{n}{\bf v}_{n}． $

よって
$\displaystyle T({\bf a}) = T({\bf b})$ $\displaystyle \Longrightarrow$ $\displaystyle T(c_{1}{\bf v}_{1} + \cdots + c_{n}{\bf v}_{n}) = T(d_{1}{\bf v}_{1} + \cdots + d_{n}{\bf v}_{n})$  
  $\displaystyle \Longrightarrow$ $\displaystyle c_{1}T({\bf v}_{1}) + \cdots + c_{n}T({\bf v}_{n}) = d_{1}T({\bf v}_{1}) + \cdots + d_{n}T({\bf v}_{n})$  
  $\displaystyle \Longrightarrow$ $\displaystyle c_{1}{\bf w}_{1} + \cdots + c_{n}{\bf w}_{n} = d_{1}{\bf w}_{1} + \cdots + d_{n}{\bf w}_{n}$  
  $\displaystyle \Longrightarrow$ $\displaystyle c_{1} = d_{1}, \ldots , c_{n} = d_{n}$  
  $\displaystyle \Longrightarrow$ $\displaystyle {\bf a} = {\bf b}$  

となり $ T$ は単射．つぎに $ {\mathbf y} \in {\mathcal R}^{n}$ とすると, $ {\mathbf y} = c_{1}{\bf w}_{1} + \cdots + c_{n}{\bf w}_{n}$ と表され, これは $ c_{1}{\bf v}_{1} + \ldots + c_{n}{\bf v}_{n}$ の $ T$ による像である．よって $ T$ は全射である．これより $ T$ は全単射な線形写像となり $ T$ は同型写像であることが示せた．
$ (2) \Rightarrow (3)$
$ T({\bf a}) = {\bf0}$ とすると $ T({\bf0}) = {\bf0} = T({\bf a}) $ となるので, 仮定より $ {\bf a} = {\bf0}$．よって $ \ker(T) = \{{\bf0}\}$. また$ T$ は全射であるから $ Im(T) = {\mathcal R}^{n}$ となる．
$ (3) \Rightarrow (4)$
$ T$ が同型写像なので $ {\bf w}_{i},{\bf w}_{j} \in R^{n}$ に対して, $ T({\bf v}_{i}) = {\bf w}_{i}, T({\bf v}_{j}) = {\bf w}_{j}$ となる $ {\bf v}_{i},{\bf v}_{j} \in V$ が存在する．また$ T$ の線形性により

$\displaystyle T(\alpha{\bf v}_{i} + \beta{\bf v}_{j}) = \alpha T({\bf v}_{i}) + \beta T({\bf v}_{j}) = \alpha {\bf w}_{i} + \beta {\bf w}_{j}.$

よって

$\displaystyle T^{-1}(\alpha {\bf w}_{i} + \beta {\bf w}_{j}) = \alpha{\bf v}_{i} + \beta{\bf v}_{j}. $

次に $ T^{-1}$ が全単射であることを示す．まず $ T^{-1}({\bf w}_{i}) = T^{-1}({\bf w}_{j})$より $ {\bf w}_{i} = {\bf w}_{j}$ を示す．

$\displaystyle {\bf w}_{i} - {\bf w}_{j} = T({\bf v}_{i}) - T({\bf v}_{j}) = T({\bf v}_{i} - {\bf v}_{j}) = T({\bf0}) = {\bf0} . $

最後に $ Im(T) = {\mathcal R}^{n}$より

$\displaystyle {\bf v}_{i} = T^{-1}({\bf w}_{i}) . $

よって $ T^{-1}$ は同型写像．
$ (4) \Rightarrow (5)$
$ \{T^{-1}({\bf w}_{1}),T^{-1}({\bf w}_{2}), \ldots , T^{-1}({\bf w}_{n})\}$ が $ V$ の基底であることを示すには, この組が1次独立でかつこの組のベクトルで張られる空間が $ V$ であることを示せばよい．

$\displaystyle c_{1}T^{-1}({\bf w}_{1})+c_{2}T^{-1}({\bf w}_{2}) + \cdots + c_{n}T^{-1}({\bf w}_{n}) = {\bf0} $

より

$\displaystyle T^{-1}(c_{1}{\bf w}_{1}+c_{2}{\bf w}_{2} + \cdots + c_{n}{\bf w}_{n}) = {\bf0}. $

ここで $ T^{-1}$ は同型写像なので

$\displaystyle c_{1}{\bf v}_{1} + c_{2}{\bf v}_{2} + \cdots + c_{n}{\bf v}_{n} = {\bf0}. $

このとき, $ \{{\bf v}_{1},\ldots,{\bf v}_{n}\}$ は1次独立であるから $ c_{1} = c_{2} = \cdots = c_{n} = 0$ を得る．よって

$\displaystyle \{T^{-1}({\bf w}_{1}),T^{-1}({\bf w}_{2}), \ldots , T^{-1}({\bf w}_{n})\} $

は1次独立である．つぎに $ {\bf v} \in V$ とすると,

$\displaystyle {\bf v} = c_{1}{\bf v}_{1} + \cdots + c_{n}{\bf v}_{n} = c_{1}T^{-1}({\bf w}_{1}) + \cdots + c_{n}T^{-1}({\bf w}_{n}) . $

よって $ \langle{\bf w}_{1},{\bf w}_{2},\ldots,{\bf w}_{n}\rangle = V$.
$ (5) \Rightarrow (1)$
$ \{T^{-1}({\bf w}_{1}),T^{-1}({\bf w}_{2}), \ldots , T^{-1}({\bf w}_{n})\}$ は $ V$ の基底より $ \dim V = n$. $ \blacksquare$

このように $ n$ 次元のベクトル空間$ V$ は $ {\mathcal R}^{n}$ と同型となるので, $ V$ のベクトル間の関係は同型写像によって $ {\mathcal R}^{n}$ のベクトル間の関係として扱うことができます．

$ \spadesuit$行列表現 $ \spadesuit$

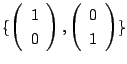有限次元のベクトル空間の線形写像を調べるために, 線形写像に行列を対応させることがあります．このとき, 線形写像の性質は行列の性質として, より具体的に表されます．たとえば, $ xy$平面上の点 $ (x,y)$ を $ \theta$だけ回転して点 $ (X,Y)$ に対応させる線形変換$ T$ を考えてみましょう．まず, $ R^2$ の1組の基底 $ \{\left(\begin{array}{c} 1\\ 0 \end{array}\right), \left(\begin{array}{c} 0\\ 1 \end{array}\right) \}$ を考えます． これより

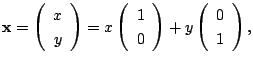
$\displaystyle {\mathbf x} = \left(\begin{array}{c} x\\ y \end{array}\right) = ... ...\\ 0 \end{array}\right) + y \left(\begin{array}{c} 0\\ 1 \end{array}\right), $


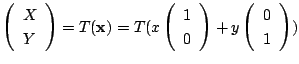$\displaystyle {\mathbf y}$ $\displaystyle =$ $\displaystyle \left(\begin{array}{c} X\\ Y \end{array}\right) = T({\mathbf x})... ...1\\ 0 \end{array}\right) + y \left(\begin{array}{c} 0\\ 1 \end{array}\right))$  
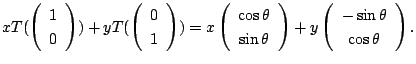  $\displaystyle =$ $\displaystyle xT(\left(\begin{array}{c} 1\\ 0 \end{array}\right) ) + y T(\left... ...) + y \left(\begin{array}{c} -\sin{\theta}\\ \cos{\theta} \end{array}\right) .$  

よって

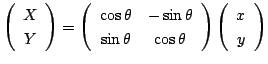
$\displaystyle \left(\begin{array}{c} X\\ Y \end{array}\right) = \left(\begin{a... ...os{\theta} \end{array}\right) \left(\begin{array}{c} x\\ y \end{array}\right) $

と行列を用いて表せます．一般に, 線形写像 $ T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{m}$ を考え,

$\displaystyle \{{\bf v}_{1},\ldots,{\bf v}_{n}\}, \{{\bf w}_{1},\ldots,{\bf w}_{m}\}$

をそれぞれ $ {\mathcal R}^{n},{\mathcal R}^{m}$ の1組の基底とし, 任意の $ {\mathbf x} \in {\mathcal R}^{n}$ とその像 $ {\mathbf y} = T({\mathbf x}) \in {\mathcal R}^{m}$ を

$\displaystyle {\mathbf x} = {\bf v}_{1}x_{1} + {\bf v}_{2}x_{2} + \cdots + {\bf v}_{n}x_{n}, $

$\displaystyle {\mathbf y} = {\bf w}_{1}y_{1} + {\bf w}_{2}y_{2} + \cdots + {\bf w}_{m}y_{m} $

と表すとき, 写像$ T$ の線形性により
$\displaystyle {\mathbf y} = T({\mathbf x})$ $\displaystyle =$ $\displaystyle T({\bf v}_{1}x_{1} + {\bf v}_{2}x_{2} + \cdots + {\bf v}_{n}x_{n})$  
  $\displaystyle =$ $\displaystyle T({\bf v}_{1})x_{1} + T({\bf v}_{2})x_{2} + \cdots + T({\bf v}_{n})x_{n}$  

となります．ここで $ \{T({\bf v}_{1}),\ldots,T({\bf v}_{n})\}$ は $ {\mathcal R}^{m}$ に含まれるので,

$\displaystyle T({\bf v}_{i}) = a_{1i}{\bf w}_{1} + a_{2i}{\bf w}_{2} + \cdots + a_{mi}{\bf w}_{m} (i = 1,2,\ldots,n)$

と表せます．これより
$\displaystyle {\mathbf y}$ $\displaystyle =$ $\displaystyle (a_{11}{\bf w}_{1} + a_{21}{\bf w}_{2} + \cdots + a_{m1}{\bf w}_{m})x_{1}$  
  $\displaystyle +$ $\displaystyle (a_{12}{\bf w}_{1} + a_{22}{\bf w}_{2} + \cdots + a_{m2}{\bf w}_{m})x_{2}$  
  $\displaystyle +$ $\displaystyle \vdots$  
  $\displaystyle +$ $\displaystyle (a_{1n}{\bf w}_{1} + a_{2n}{\bf w}_{2} + \cdots + a_{mn}{\bf w}_{m})x_{n}$  

となります．ここで $ \{{\bf w}_{1},{\bf w}_{2},\ldots,{\bf w}_{m}\}$ は $ {\mathcal R}^{m}$ の基底をなしているので, 対応する係数は等しいはずです．よって次のような関係式が得られます．

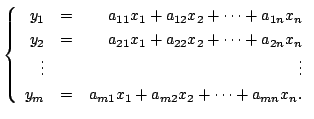
$\displaystyle \left \{ \begin{array}{rrr} y_{1}& =& a_{11}x_{1} + a_{12}x_{2} +... ...{m}& =& a_{m1}x_{1} + a_{m2}x_{2} + \cdots + a_{mn}x_{n} . \end{array}\right . $

これより右辺の係数行列 $ A = (a_{ij})$ が定まります．この行列 $ A$ を基底

$\displaystyle \{{\bf v}_{1},\ldots,{\bf v}_{n}\}, \{{\bf w}_{1},\ldots,{\bf w}_{m}\}$

に関する $ T$ の 行列表現(matrix representation) といい $ [T]_{\bf v}^{\bf w}$ と表します．とくに $ V = W$ の場合は, 通常 $ \{{\bf v}_{1},\ldots,{\bf v}_{n}\}$ と $ \{{\bf w}_{1},\ldots,{\bf w}_{n}\}$ とを同一にとり $ T$ の行列表現を $ [T]_{\bf v}$ と表します．また $ T: { R}^{n} \longrightarrow { R}^{n}$ のとき, 標準基底(usual basis)

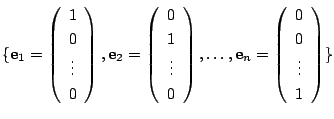
$\displaystyle \{{\bf e}_{1} = \left(\begin{array}{c} 1\\ 0\\ \vdots\\ 0 \end... ...\bf e}_{n} = \left(\begin{array}{c} 0\\ 0\\ \vdots\\ 1 \end{array}\right)\} $

を用いて $ T$ の行列表現は $ [T]_{\bf e}$ または $ [T]$ で表します．

ここまでをまとめると $ {\mathcal R}^{n}$ から $ {\mathcal R}^{m}$ への線形写像$ T$ は, $ {\mathcal R}^{n}$ の基底の像を $ {\mathcal R}^{m}$ の基底で表したとき, $ m \times n$型の行列 $ A$ で表され,

$\displaystyle [T({\mathbf x})]_{\bf w} = [T]_{\bf v}^{\bf w}[{\mathbf x}]_{\bf v} $

を満たします．

例題 3.3   $ T : {\mathcal R}^{2} \longrightarrow {\mathcal R}^{2}$ が $ T\left(\begin{array}{c} x\\ y \end{array}\right) = \left(\begin{array}{c} 3x - 4y\\ x + 5y \end{array}\right)$ で与えられているとき, 標準基底 $ \{{\bf e}_{1},{\bf e}_{2}\}$ に関する $ T$ の行列表現$ [T]$ と基底 $ \{{\bf w}_{1} = \left(\begin{array}{c} 1\\ 3 \end{array}\right), {\bf w}_{2} = \left(\begin{array}{c} 2\\ 5 \end{array}\right)\}$ に関する $ T$ の行列表現 $ [T]_{\bf w}$ を求めよ．また基底 $ \{{\bf e}_{1},{\bf e}_{2}\}, \{{\bf w}_{1},{\bf w}_{2}\}$ に関する $ T$ の行列表現 $ [T]_{\bf e}^{\bf w}$ を求めよう．

解

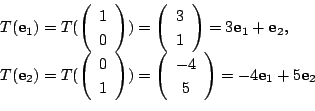
\begin{displaymath}\begin{array}{l} T({\bf e}_{1}) = T(\left(\begin{array}{c} 1\... ...5 \end{array}\right) = -4{\bf e}_{1} + 5{\bf e}_{2} \end{array}\end{displaymath}

より $ [T] = \left(\begin{array}{cc} 3&-4\\ 1&5 \end{array}\right)$.
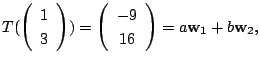$\displaystyle T({\bf w}_{1})$ $\displaystyle =$ $\displaystyle T(\left(\begin{array}{c} 1\\ 3 \end{array}\right)) = \left(\begin{array}{c} -9\\ 16 \end{array}\right) = a{\bf w}_{1} + b{\bf w}_{2},$  
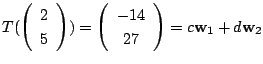$\displaystyle T({\bf w}_{2})$ $\displaystyle =$ $\displaystyle T(\left(\begin{array}{c} 2\\ 5 \end{array}\right)) = \left(\begin{array}{c} -14\\ 27 \end{array}\right) = c{\bf w}_{1} + d{\bf w}_{2}$  

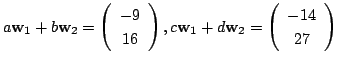とおくと $ a{\bf w}_{1} + b{\bf w}_{2} = \left(\begin{array}{c} -9\\ 16 \end{array}\righ... ...\bf w}_{1} + d{\bf w}_{2} = \left(\begin{array}{c} -14\\ 27 \end{array}\right)$より $ a = 77,b = -43, c = 124, d = -69$ を得る．よって $ [T]_{\bf w} = \left(\begin{array}{cc} 77&124\\ -43&-69 \end{array}\right)$.
また
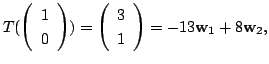$\displaystyle T({\bf e}_{1})$ $\displaystyle =$ $\displaystyle T(\left(\begin{array}{c} 1\\ 0 \end{array}\right)) = \left(\begin{array}{c} 3\\ 1 \end{array}\right) = -13{\bf w}_{1} + 8{\bf w}_{2},$  
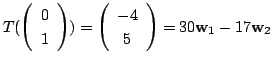$\displaystyle T({\bf e}_{2})$ $\displaystyle =$ $\displaystyle T(\left(\begin{array}{c} 0\\ 1 \end{array}\right)) = \left(\begin{array}{c} -4\\ 5 \end{array}\right) = 30{\bf w}_{1} - 17{\bf w}_{2}$  

より $ [T]_{\bf e}^{\bf w} = \left(\begin{array}{cc} -13&30\\ 8&-17 \end{array}\right)$. $ \blacksquare$

$ \spadesuit$次元公式 $ \spadesuit$

線形写像の行列表現を用いて, もう一度線形写像の核と像について調べてみましょう．線形写像$ T$ を $ T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{m}$ とします．このとき$ \ker(T)$ は $ T$ の像が $ {\bf0}$ になる $ {\mathcal R}^{n}$ の要素の集まりでした．つまり連立1次方程式

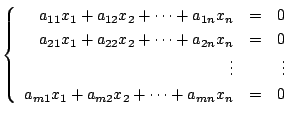
$\displaystyle \left \{ \begin{array}{rrr} a_{11}x_{1} + a_{12}x_{2} + \cdots + ... ...\ a_{m1}x_{1} + a_{m2}x_{2} + \cdots + a_{mn}x_{n}& = & 0 \end{array}\right . $

の解からつくられる解空間と同じになります．また定理2.9より, 解空間の次元は

$\displaystyle \dim \ker(T) = n - {\rm rank}(A)$

となります．では $ Im(T)$ はどうでしょうか．$ Im(T)$ は $ {\mathcal R}^{n}$ のすべての元の像の集まりなので $ \dim Im(T) = {\rm rank}(A)$ となります．これから次元公式とよばれる次の定理を得ます．

定理 3.2   $ T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{m}$ を線形写像とするとき,

$\displaystyle \dim {\mathcal R}^{n} = \dim \ker(T) + \dim Im(T) $

が成り立つ．

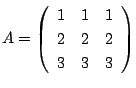例題 3.4   $ T : {\mathcal R}^{3} \longrightarrow {\mathcal R}^{3}$ の行列表現を $ A = \left(\begin{array}{rrr} 1&1&1\\ 2&2&2\\ 3&3&3 \end{array}\right )$ とするとき, $ \dim \ker(T)$ を求めよう．

解 $ \dim \ker(T)$ は $ \dim {\mathcal R}^{3} - \dim Im(T)$ と等しく, $ \dim Im(T) = {\rm rank}(A)$より $ {\rm rank}(A)$ を求めれば $ \dim \ker(T)$ が求まる．

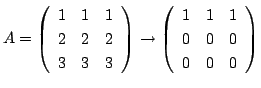
$\displaystyle A = \left(\begin{array}{rrr} 1&1&1\\ 2&2&2\\ 3&3&3 \end{array}\... ...ightarrow \left(\begin{array}{rrr} 1&1&1\\ 0&0&0\\ 0&0&0 \end{array}\right ) $

より $ {\rm rank}(A) = 1$. したがって $ \dim \ker(T) = 3 - 1 = 2$. $ \blacksquare$

ベクトル空間 $ ,{\mathcal R}^{l},{\mathcal R}^{n},{\mathcal R}^{m}$ の間に線形写像

$\displaystyle S : { R}^{l} \longrightarrow {\mathcal R}^{n}, T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{m} $

が与えられたとき, その合成写像 $ T \circ S : { R}^{l} \longrightarrow { R}^{m}$も線形写像となりました(例題3.2)．そこで各空間に基底をとり, それらに関する $ S,T$ の行列を $ A,B$ とすると $ {\mathbf x} = (x_{i}), {\mathbf y} = (y_{j}), {\mathbf z} = (z_{k})$ に対して

$\displaystyle (y_{i}) = A(x_{j}), (z_{k}) = B(y_{i}) = BA(x_{j}) $

となるので $ T \circ S$ の行列表現は $ BA$ となります．

定理 3.3   線形変換 $ T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{n}$ の基底 $ \{{\bf v}_{i}\}$ に関する行列表現を $ A$ とするとき, 次の条件は同値である．
$ (1)$ $ T$ は同型写像である．
$ (2)$ 行列 $ A$ は正則行列である．

証明 $ (1) \Rightarrow (2)$
$ T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{n}$ の行列表現を $ A$ とする．$ T$ は同型写像より $ T^{-1}$ が存在する．$ T^{-1}$ の行列表現を $ B$ とすると, $ BA = I$ が成り立つから, $ A$ は正則行列である．
$ (2) \Rightarrow (1)$
$ A$ が正則行列ならば$ BA = I$ となる行列が存在し, この $ B$ に対する写像を $ S$すると $ T \circ S = 1$．よって, 演習問題3.1より $ T$ は同型写像． $ \blacksquare$

演習問題3-2

1. 次の写像のうち線形写像はどちらか．

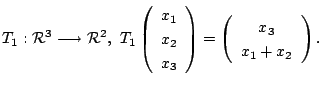
$\displaystyle T_{1} : {\mathcal R}^{3} \longrightarrow {\mathcal R}^{2}, T_{1}... ...y}\right) = \left(\begin{array}{c} x_{3}\\ x_{1} + x_{2} \end{array}\right) . $

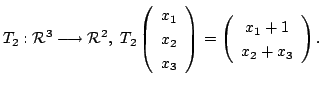
$\displaystyle T_{2} : {\mathcal R}^{3} \longrightarrow {\mathcal R}^{2}, T_{2}... ...ight) = \left(\begin{array}{c} x_{1} + 1\\ x_{2} + x_{3} \end{array}\right) . $

2. $ V$ は $ n$ 次元ベクトル空間, $ \{{\bf v}_{1},\ldots,{\bf v}_{n}\}$ を $ V$ の基底とする． $ T : V \longrightarrow {\mathcal R}^{n}$ を $ T(\alpha_{1}{\bf v}_{1} + \alpha_{2}{\bf v}_{2} + \cdots + \alpha_{n}{\bf v}_{... ... \alpha_{1}{\bf e}_{1} + \alpha_{2}{\bf e}_{2} + \cdots + \alpha_{n}{\bf e}_{n}$ と定義すると, $ T$ は線形写像になることを示せ．

3. 線形写像 $ T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{n}$ について, 次の条件は同値であることを証明せよ．

(a)
$ T$ は同型写像である．
(b)
$ T \circ S = 1$ を満たす線形写像 $ S : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{n}$ が存在する．

4. $ T : V \longrightarrow W$ が線形写像のとき, $ \ker(T),Im(T)$ は $ V,W$ の部分空間であることを示せ．

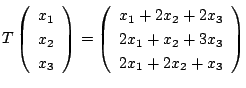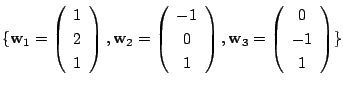5. $ T : {\mathcal R}^{3} \longrightarrow {\mathcal R}^{3}$ が $ T\left(\begin{array}{r} x_{1}\\ x_{2}\\ x_{3} \end{array}\right) = \left(\be... ...x_{3}\\ 2x_{1} + x_{2} + 3x_{3}\\ 2x_{1} + 2x_{2} + x_{3} \end{array}\right) $ のとき, 標準基底 $ \{{\bf e}_{1},{\bf e}_{2},{\bf e}_{3}\}$ に関する $ T$ の行列表現$ [T]$ と基底 $ \{{\bf w}_{1} = \left(\begin{array}{c} 1\\ 2\\ 1 \end{array}\right), {\bf w}... ...\right), {\bf w}_{3} = \left(\begin{array}{c} 0\\ -1\\ 1 \end{array}\right)\}$ に関する行列表現 $ [T]_{\bf w}$ を求めよ．
また $ \dim \ker(T)$ を求めよ．

next up previous contents index
: 行列の変換と固有値 : 線形写像 : 線形写像   目次   索引
yokotalab 平成20年3月7日