Next: Space curves Up: Introduction to Vector Analysis Previous: Vector triple product Contents Index
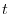 belonging to the subset
belonging to the subset 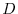 of the real
of the real  , given the real functions
, given the real functions
 , one vector you can think of
, one vector you can think of
 .This vector
.This vector
 is called one variable vector-valued function or vector function from
is called one variable vector-valued function or vector function from 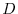 to
to  and denoted by
and denoted by


Often
 is geometrically a mapping from the real axis
is geometrically a mapping from the real axis 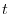 to the vector connecting the origin and the point
to the vector connecting the origin and the point
 . It will be treated.
. It will be treated.
 ,find the trace of
,find the trace of
 .
.
Answer
The components of
 are
are
 . Then
. Then
 and the trace of
and the trace of
 ,
,
 is on the paraboloid
is on the paraboloid
 .
.
|
Since the definition of the limit value is the same as for the one-variable function, you probably expect the definition of continuity to be the same as for the one-variable function. In fact, that's the case.
|
In this way, various definitions in a one-variable function are inherited by a vector function.
|
We will study in the next chapter, the direction of the vector
 is the direction of the tangent line to the curve
is the direction of the tangent line to the curve
 .
.
As the sum of vectors and the scalar multiple are defined by the sum of the corresponding components and the scalar multiple, the calculation of the limit value, derivative coefficient, and indefinite integral of the vector function is performed by the limit value, derivative coefficient, of the component of the vector function. It can be obtained from the indefinite integral.
Proof
(a)
 |
 |
 |
 ,then
,then
 .Also,if
.Also,if
 ,
,


 implies
implies

Proof of (b),(c),(d) are your exercise. .
 , find
, find
 .
.
Answer Differentiate eachcomponents, we have

If

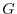
 are differentiable for
are differentiable for 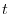 , then the followings are true.
, then the followings are true.
|

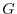
 ,find the followings:.
(1)
,find the followings:.
(1)

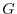
 (2)
(2)

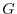
 Answer
Answer
 .
.
(1)
 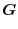  |
 |
 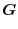  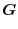  |
|
 |
 |
||
 |
 |
 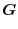  |
 |
 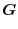  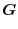  |
|
 |
 |
||
 |
 |
||
 |
 |
 ,
,
 is constant,show that
is constant,show that
 and
and
 are orthogonal for all
are orthogonal for all 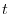 .
.
Answer
Let
 . Then
. Then
 .
Thus, by the derivative of the vector function, we have
.
Thus, by the derivative of the vector function, we have

 and
and
 are orthogonal.
are orthogonal.
For every vector functions  and a constant
and a constant  ,a constant vector
,a constant vector
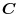 , we have the followings:
, we have the followings:
|
 ,prove that
,prove that
 .
Answer
.
Answer
 .Therefore,,
.Therefore,,
 .
.
 , provide
, provide
