Next: Exercise Answer Up: Integral formula Previous: Gauss's divergence theorem Contents Index
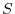 and its boundary
and its boundary 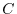 in the common domain of the scalar fields
in the common domain of the scalar fields 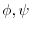 ..
..

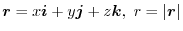 and
and  be a scalar field. Then prove the following equation holds for any surface
be a scalar field. Then prove the following equation holds for any surface 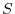 and its boundary
and its boundary 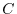 .
.



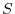 and its boundary
and its boundary 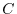 in the common domain of the scalar field
in the common domain of the scalar field  and the vector field
and the vector field  .
.

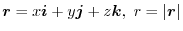 and
and  be a scalar field. Prove that for any surface
be a scalar field. Prove that for any surface 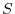 and its boundary
and its boundary 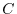 , the following equation holds.
, the following equation holds.

 is defined in the whole space..About the border
is defined in the whole space..About the border 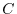 of any curved surface if
of any curved surface if

 has a scalar potential. Prove this.
has a scalar potential. Prove this.
 ,show that Stokes' theorem holds.
,show that Stokes' theorem holds.
 .where
.where 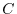 is a curve connecting from the point
is a curve connecting from the point  to
to  and back to the starting point..
and back to the starting point..
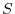 and its boundary
and its boundary 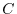 within the common domain of
within the common domain of
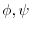 , prove the following equation holds.
, prove the following equation holds.

9.
Let
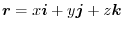 .Prove for any surface
.Prove for any surface 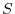 and its boundary
and its boundary 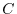 , the following is true.
, the following is true.

