Next: Numerical Analysis Up: 1st order linear differential Previous: Linear Differential Equations 目次 索引
2. Solve the following differential equations.
3. Solve the following differential equations.
(a)
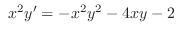 , Note that
, Note that
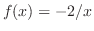 is a solution
is a solution
(b)
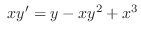
Answer
1.
(a) Rewrite into the standard form.
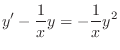
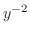 to the both sides.
to the both sides.
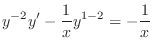
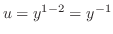 . Then
. Then
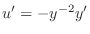 implies that
implies that
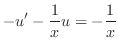
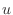 . Thus rewrite this into the standard form in
. Thus rewrite this into the standard form in 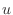 . Then
. Then
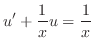
 . Then
. Then
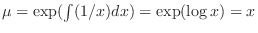 る. Multiply
る. Multiply  to the standard form. Then the left-hand side is the derivative of the product of
to the standard form. Then the left-hand side is the derivative of the product of  and the dependent variable
and the dependent variable 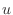 .
.
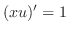
 . Then
. Then
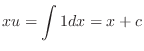
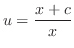
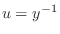 , we have
, we have
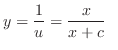
(b) Rewrite into the standard form.
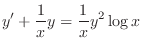
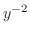 to the both sides.
to the both sides.
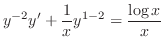
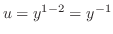 . Then
. Then
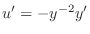 and
and
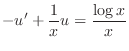
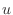 . Write this into the standard form in
. Write this into the standard form in 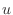 .
.
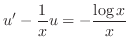
 . Then
. Then
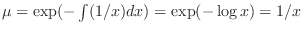 . Multiply
. Multiply 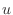 to the standard form. The left-hand side is the derivative of the product of
to the standard form. The left-hand side is the derivative of the product of  and
and 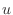 . Then
. Then
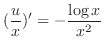
 .
.
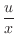 |
 |
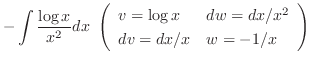 |
|
 |
![$\displaystyle - [- \frac{\log{x}}{x} - \int \frac{-1}{x^2} dx ] = \frac{\log{x}}{x} + \frac{1}{x} + c$](img493.png) |
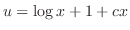 and
and
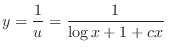
(c) Rewrite this into the standard form.
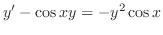
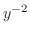 and simplify
and simplify
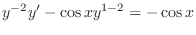
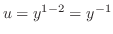 . Then we have
. Then we have
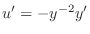 and
and
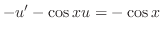
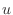 . Now write inot the standard form in
. Now write inot the standard form in 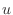 .
.
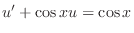
 . Note that
. Note that
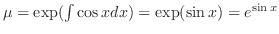 . Multiply
. Multiply  to the standard form. Then the left-hand side is the derivative of the product of
to the standard form. Then the left-hand side is the derivative of the product of  and
and 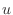 .
.
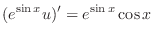
 . We have
. We have
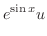 |
 |
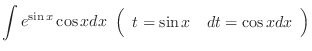 |
|
 |
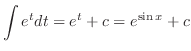 |
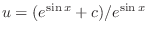 and
and
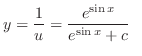
2. (a) Rewrite into the standard form.
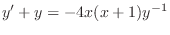
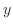 to both sides.
to both sides.
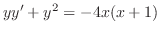
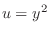 . Then
. Then
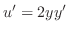 and
and
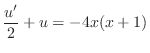
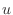 . So, write into the standard form in
. So, write into the standard form in 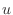 .
.
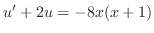
 . Note that
. Note that
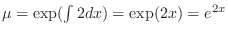 . Then multiply
. Then multiply 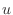 to the standard form,The left-hand side is the derivative of the product of
to the standard form,The left-hand side is the derivative of the product of  and
and 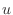 .
.
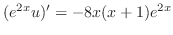
 .
.
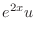 |
 |
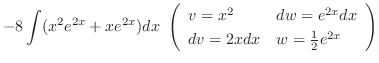 |
|
 |
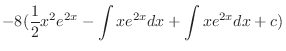 |
||
 |
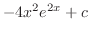 |
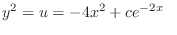
(b) In
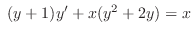 ,we let
,we let
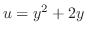 . Then
. Then
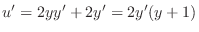 . Now put this back into the original equation.
. Now put this back into the original equation.
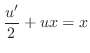
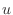 . So, write this into the standard form in
. So, write this into the standard form in 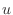 .
.
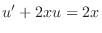
 . Then
. Then
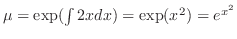 . Then multiply this to the standard form. Then the left-hand side is the derivative of the product of
. Then multiply this to the standard form. Then the left-hand side is the derivative of the product of  and
and 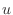 .
.
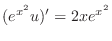
 .
.
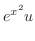 |
 |
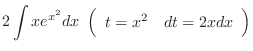 |
|
 |
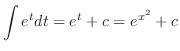 |
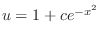 and
and
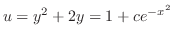
3. (a) Rewrite this into the standard form.
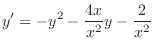
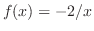 is a solution of the above differential equation, let
is a solution of the above differential equation, let
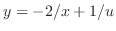 . Then
. Then
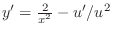 . Write this into the standard form.
. Write this into the standard form.
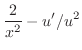 |
 |
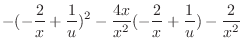 |
|
 |
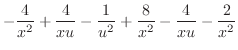 |
||
 |
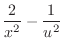 |
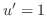 . Therefore,
. Therefore,
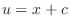
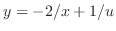 , we have
, we have
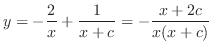
(b) Rewrite this into the standard form
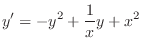
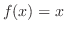 is a solution of this equation. We let
is a solution of this equation. We let
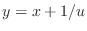 . Then
. Then
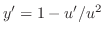 . Put these back into the standard form.
. Put these back into the standard form.
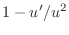 |
 |
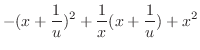 |
|
 |
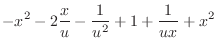 |
||
 |
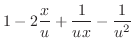 |
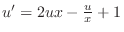 . This is a linear differential equation. So, write in the standard form.
. This is a linear differential equation. So, write in the standard form.
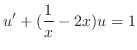
 , we have
, we have
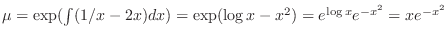 . Multiplying
. Multiplying  to the standard form in
to the standard form in 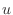 . Then the left-hand side is the derivative of the product of
. Then the left-hand side is the derivative of the product of  and
and 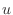 . Thus,
. Thus,
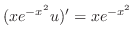
 .
.
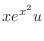 |
 |
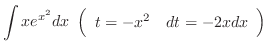 |
|
 |
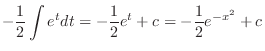 |
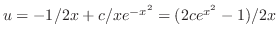 . Hence,
. Hence,