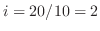Next: Bernoulli,Riccati's Differential Equations Up: 1st order linear differential Previous: Integrating Factor 目次 索引
(a)
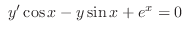
(b)
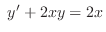
(c)
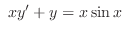
(d)
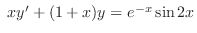
2. Solve the following initial value problems.
(a)
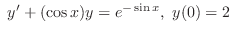
(b)
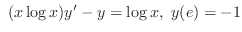
(c)
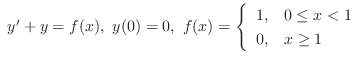
(d)
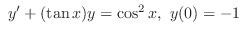
3. Given RL circuit with 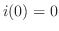 .
.
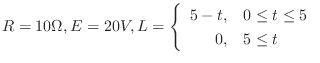
1. (a) This is a linear diffenretial equation. Now write this in the standard form.
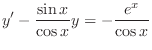
 is given by
is given by
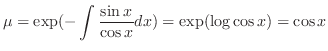
 to the standard form. Then
to the standard form. Then
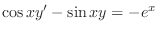
 times the dependent variable
times the dependent variable 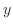 . Then
. Then
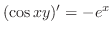
 .
.
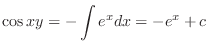
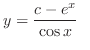
(b) This equation is a linear differential equation. So, the integrating factor  is given by
is given by
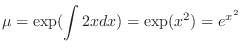
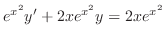
 times
times 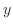 .
.
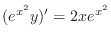
 , we have
, we have
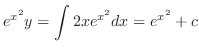
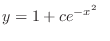
(c) This equation is a linear differntial equation. So, write in the standard form. Then
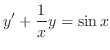
 is
is
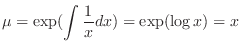
 to the standard form. Then we have
to the standard form. Then we have
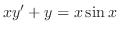
 times
times 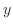 .
.
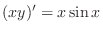
 .
.
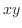 |
 |
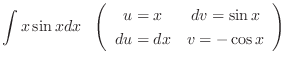 |
|
 |
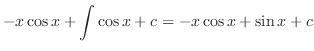 |
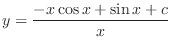
(d) This equation is a linear differential equation. Now write in the standard form. Then
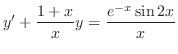
 is
is
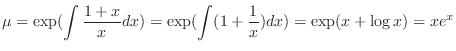
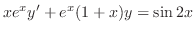
 times
times 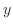 .
.
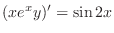
 .
.
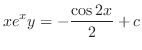
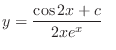
2.
(a) This equation is a linear differential equation. The integrating factor  is given by
is given by
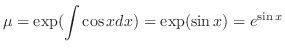
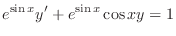
 times
times 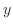 .
.
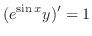
 .
.
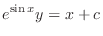
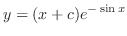
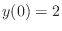 , we have
, we have
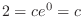 and
and
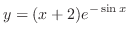
(b) This equation is a linear differential equation. So, write in the standard form.
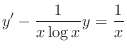
 is
is
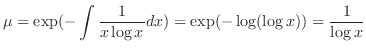
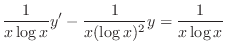
 times
times 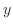 .
.
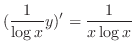
 . Then
. Then
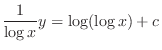
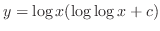
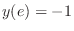 , we have
, we have
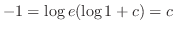 and
and
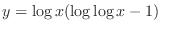
(c) This equation is a linear differential equation. So, the integrating factor  is given by
is given by
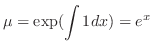
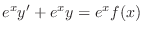
 times
times 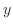 .
.
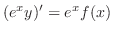
 , we have
, we have
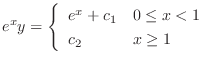
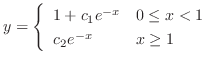
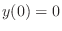 , we have
, we have
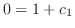 and
and
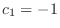 .Thus, for
.Thus, for
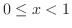 ,
,
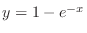 . Note that the solution of this differential equation must be continuous. Then
. Note that the solution of this differential equation must be continuous. Then
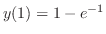 and
and
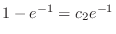 .Thus,
.Thus,
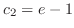 . From this, we have
. From this, we have
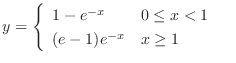
(d) This equation is a linear differential equation. Then the integrating factor  is
is
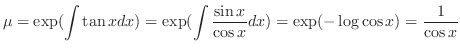
 to the standard form. Then
to the standard form. Then
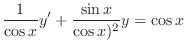
 and
and 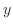 .
.
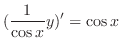
 .
.
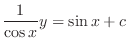
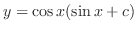
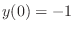 , we have
, we have
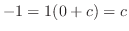 and
and
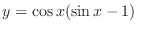
3. The differential equation for the current running through RL-circuit is
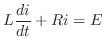
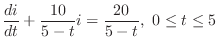
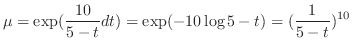
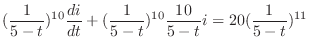
 and
and 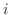 .
.
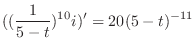
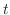 .
.
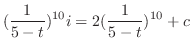
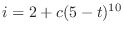
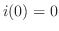 . Then we have
. Then we have
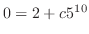 and
and
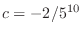 . Therefore,
. Therefore,
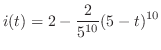
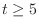 . Since
. Since 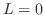 , the differential equation for the current running through RL-circuit is
, the differential equation for the current running through RL-circuit is
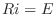 and
and