Jordan Cannonical Form

$\spadesuit$Jordan block $\spadesuit$

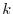The $k$th square matrix is said to be Jordan block for the complex number $\alpha$.

$$J(\alpha,k) = \left(\begin{array}{ccccc} \alpha & 1 & & 0& \\ ... ...dots & \ddots & \\ & & & \alpha & 1\\ & 0 & & & \alpha \end{array}\right)$$

Example 5..1  

Represent the following Jordan block. $J(5,1), J(6,2), J(5,3)$

Answer

$$j(5,1) = (5), J(6,2) = \left(\begin{array}{cc} 6 & 1\\ 0 & 6 ... ...5,3) = \left(\begin{array}{ccc} 5&1&0\\ 0&5&1\\ 0&0&5 \end{array}\right)$$

Matrix obtained by arranging several Jordan blocks diagonally

$$J = \left(\begin{array}{cccc} J(\alpha_{1},k_{1}) & & &\\ & J(... ...2},k_{2}) & & \\ & & \ddots &\\ &0&&J(\alpha_{i},k_{i}) \end{array}\right)$$

is called Jordan form.

$\spadesuit$Standard form of nilpotent matrix $\spadesuit$

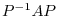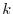Can any $n$ square matrix $A$ take the appropriate regular matrix $P$ and make $P^{-1}AP$ a Jordan matrix?. First, consider the case where $$ is a nilpotent matrix. Let $N$ be a nilpotnet matrix. Then by the definition of the nilpotent matrix, there exists an integer $k$ which satisfies $N^{k-1} \neq 0, N^{k} = 0$. Now let

$$W_{j} = W_{j}(0) = \{{\mathbf x} \in {\mathcal C}^{n} : N^{j}{\mathbf x} = {\bf0}\}$$

Then consider the sequaence of subspaces

$$V(0) = W_{1} \subset W_{2} \subset \cdots \subset W_{k} = {\mathcal C}^{n}$$

Now let

$$g_{i} = \dim W_{i} (1 \leq i \leq k)$$

$$h_{k} = g_{k} - g_{k-1}, h_{k} + h_{k+1} = g_{k-1} - g_{k-2}$$

$$h_{k} + h_{k-1} + h_{k-2} = g_{k-2} - g_{k-3}, \ldots,$$

and let ${\mathbf x}_{1}, \ldots ,{\mathbf x}_{h_{k}}$ be the linearly independent vectors in $W_{k}$ satisfies

$$<{\mathbf x}_{1}, \ldots , {\mathbf x}_{h_{k}}> \bigcap W_{k-1} = {\bf0}$$

Then the following $kh_{k}$ vectors

$$\left\{\begin{array}{l} {\mathbf x}_{1}, N{\mathbf x}_{1},\ldots,... ...{\mathbf x}_{h_{k}},\ldots,N^{k-1}{\mathbf x}_{h_{k}} \end{array}\right. *$$

are linearly independent. Because letting the linear combination of these vectors be equal to 0, then

$$\sum_{i=1}^{h_{k}}c_{i}^{0}{\mathbf x}_{i} + \sum_{i=1}^{h_{k}}c_... ..._{i} + \cdots + \sum_{i=1}^{h_{k}}c_{i}^{h_{k}}N^{k-1}{\mathbf x}_{i} = {\bf0}$$

Now multiply $N^{[k-1]}$ to both sides of this equation from the left. Then the sum of terms after the 2nd term is 0 and we have

$$\sum_{i=1}^{h_{k}}c_{i}^{0}N^{k-1}{\mathbf x}_{i} = N^{k-1}\left(\sum_{i=1}^{h_{k}}c_{i}^{0}{\mathbf x}_{i}\right) = {\bf0}$$

Thus, $\sum_{i=1}^{h_{k}}c_{i}^{0}{\mathbf x}_{i} \in W_{k-1}$. But by the assumption

$$<{\mathbf x}_{1}, \ldots , {\mathbf x}_{h_{k}}> \bigcap W_{k-1} = {\bf0}$$

it has to be $c_{1}^{0} = \cdots = c_{h_{k}}^{0} = 0$. Similarly, repeating this process, we have $c_{i}^{j} = 0 (i = 1,\ldots,h_{k}, j = 0 , \ldots, k-1)$.

Next we conside the vectors ${\mathbf y}_{1},\ldots,{\mathbf y}_{h_{k-1}}$ satisfying the following conditions. $$\begin{array}{ll} (1) & {\mathbf y}_{1},\ldots,{\mathbf y}_{h... ...\mathbf y}_{h_{k-1}}> \bigcap W_{k-2} = \{{\bf0}\} \end{array}$$

At this time, the combination of the following $h_{k-1}$ vectors and the (*) vector is also linearly independent.

$$\left\{\begin{array}{l} {\mathbf y}_{1}, N{\mathbf y}_{1},\ldots,... ...hbf y}_{h_{k-1}},\ldots,N^{k-1}{\mathbf y}_{h_{k-1}} \end{array}\right. **$$

Similarly, we conside the vectors ${\mathbf z}_{1},\ldots,{\mathbf z}_{h_{k-2}}$.

$$\begin{array}{ll} (1) & {\mathbf z}_{1},\ldots,{\mathbf z}_{h... ...\mathbf z}_{h_{k-2}}> \bigcap W_{k-3} = \{{\bf0}\} \end{array}$$

You can repeat this discussion below, and finally the whole vector below will be the basis of ${\mathcal C}^{n}$.

$$W_{k} \! \left\{\begin{array}{ll} & {\mathbf x}_{1}, \l... ...}_{1},..,N^{k-3}{\mathbf z}_{h_{k-2}},.. \end{array}\right. \end{array}\right.$$

and each subspace is $N$-invariant.

$$\begin{array}{l} <N^{k-1}{\mathbf x}_{1},N^{k-2}{\mathbf x}_{... ...{h_{k-2}},\ldots,{\mathbf z}_{h_{k-2}}>,\\ \cdots \end{array}$$

Now we multiply $N$ to the $(n,k)$ matrix $(N^{k-1}{\mathbf x}_{1}, N^{k-2}{\mathbf x}_{1} ,\ldots,{\mathbf x}_{1})$ from the left. Then

$$N(N^{k-1}{\mathbf x}_{1}, N^{k-2}{\mathbf x}_{1} ,\ldots,{\mathbf... ... (N^{k-1}{\mathbf x}_{1}, N^{k-2}{\mathbf x}_{1} ,\ldots,{\mathbf x}_{1})J(0,k)$$

Similarly for other subspace, we let

$$P = (N^{k-1}{\mathbf x}_{1} N^{k-2}{\mathbf x}_{1} \cdots {\mat... ...{\mathbf x}_{h_{k}} N^{k-2}{\mathbf x}_{h_{k}} \cdots {\mathbf x}_{h_{k}}$$

$$N^{k-2}{\mathbf y}_{1} N^{k-3}{\mathbf y}_{1} \cdots {\math... ...{k-1}} N^{k-3}{\mathbf y}_{h_{k-1}} \cdots {\mathbf y}_{h_{k-1}} \cdots )$$

Then $P$ is a regular matrix and we have

$$P^{-1}NP = \left(\begin{array}{cccc} J(0,k_{1}) & & 0 & \\ & J(0,k_{2}) & &\\ & 0 &\ddots &\\ &&& J(0,k_{l}) \end{array}\right)$$

The Jordan matrix created in this way is called ordan canonical form of $N$. Summarizing the above, we get the following theorem

Theorem 5..3  

Let $N$ be $n$th square matrix. Then by the appropriate regular matrix $P$, we have

$$P^{-1}NP = \left(\begin{array}{cccc} J(0,k_{1}) & & 0 & \\ & J(0,k_{2}) & &\\ & 0 &\ddots &\\ &&& J(0,k_{l}) \end{array}\right)$$

Note that $n = k_{1} + k_{2} + \cdots + k_{l}$.

Example 5..2  

Find the Jordan canonical form of the following nilpotent matrix.

$$N = \left(\begin{array}{ccc} 0&1&-1\\ 0&0&0\\ 0&0&0 \end{array}\right)$$

Answer Since $N$ satisfies $N^{2} = 0$, it is a nilpotent matrix of order 2. Thus, the eigenvalue of $N$ is 0. Now consider general eigen space $W_{j}$ for the eigenvalue 0.

$$W_{j} = \{{\mathbf x} : N^{j}{\mathbf x} = {\bf0} \}$$

implies $W_{1} \subset W_{2} = {\mathcal R}^{3}$.

$$W_{1} = \{\left(\begin{array}{c} x\\ y\\ z \end{array}\right) : y - z = 0\}$$

implies $\dim W_{1} = 2$. So, we let ${\mathbf x} = \left(\begin{array}{c} 0\\ 1\\ 0 \end{array}\right)$ Then ${\mathbf x} \in W_{2}$, and

$$N{\mathbf x} = \left(\begin{array}{c} 1\\ 0\\ 0 \end{array}\right) \in W_{1}$$

Since the dimension of $W_{1}$ is 2, there is a vector ${\mathbf y} = \left(\begin{array}{c} 0\\ 1\\ 1 \end{array}\right) \in W_{1}$ which is linearly independent from $N{\mathbf x}$ Note that $\{{\mathbf x}, N{\mathbf x}, {\mathbf y}\}$ is the basis of ${\mathcal R}^{3}$. Let

$$P = (N{\mathbf x},{\mathbf x}, {\mathbf y}) = \left(\begin{array}{ccc} 1&0&0\\ 0&1&1\\ 0&0&1 \end{array}\right)$$

Then

$$P^{-1}NP = \left(\begin{array}{ccc} 0&1&0\\ 0&0&0\\ 0&0&0 \... ...right) = \left(\begin{array}{cc} J(0,2) & 0\\ 0 & J(0,1) \end{array}\right)$$

.

$\spadesuit$Jordan canonical form $\spadesuit$

Theorem 5..4  

Let $A$ be a $n$th square matrix and its characteristic polynomial be

$$\Phi_{A}(t) = (t - \lambda_{1})^{n_{1}}(t - \lambda_{2})^{n_{2}} \cdots (t - \lambda_{r})^{n_{r}}$$

and

$$\lambda_{i} \neq \lambda_{j} (i \neq j), n = n_{1}+n_{2}+\cdots+n_{r}$$

The by the appropriate regular matrix $P$, we have

$$P^{-1}AP = \left(\begin{array}{cccc} J(\lambda_{1},k_{1}) & & 0 ... ...,k_{2}) & &\\ & 0 &\ddots &\\ &&& J(\lambda_{r},k_{l}) \end{array}\right)$$

Note that $n = k_{1} + k_{2} + \cdots + k_{l}$.

Proof For the generalized eigenspace $W(\lambda_{i})$ of the eigenvalues $\lambda_{i}$, consider the sequence of subspaces

$$W_{1}(\lambda_{1}) \subset W_{2}(\lambda_{2}) \subset \cdots \subset W_{k}(\lambda_{i}) = W_{k+1}(\lambda_{i+1}) + \cdots$$ (5.2)

Note that

$$W_{j}(\lambda_{i}) = \{{\mathbf x} \in {\mathcal C}^{n} : (A - \lambda_{i}I)^{j} {\mathbf x} = {\bf0}\}$$

$$W(\lambda_{i}) = W_{k}(\lambda_{i})$$

Then $W(\lambda_{i})$ is $A$-invariant and $(A - \lambda_{i}I)$-invariant subspace of ${\mathcal C}^{n}$. Thus, we can apply the argument of the theorem 5.2 to $A - \lambda_{i}I$ and the sequence (5.2). Now the basis of $W(\lambda_{i})$ is

$$\{{\bf p}_{1}^{i},{\bf p}_{2}^{i},\ldots,{\bf p}_{n_{i}}^{i}\}$$

and the $(n,n_{i})$ matrix obtained by arrangement.

$$P_{i} = ({\bf p}_{1} {\bf p}_{2}^{i} \cdots {\bf p}_{n_{i}}^{i})$$

and

$$(A - \lambda_{i}I)P_{i} = P_{i}\left(\begin{array}{cccc} J(0,k_{... ...}^{i}) & 0&\\ & 0 & \ddots &\\ & & & J(0,k_{l_{i}}^{i}) \end{array}\right)$$

Note that we can choose $n_{i} = k_{1}^{i} + k_{2}^{i} + \cdots + k_{l_{i}}^{i}$. Now transpose $\lambda_{i}IP_{i} = \lambda_{i}P_{i}$ to the right hand, we have

$$AP_{i} = \lambda_{i}P_{i} + P_{i}\left(\begin{array}{cccc} J(0,k_{1}^{i}) ... ..._{2}^{i}) & 0&\\ & 0 & \ddots &\\ & & & J(0,k_{l_{i}}^{i}) \end{array}\right)$$

$$= P-{i}\left(\begin{array}{cccc} J(\lambda_{i},k_{1}^{i}) &&&\\ & ... ...& 0&\\ & 0 & \ddots &\\ & & & J(\lambda_{i},k_{l_{i}}^{i}) \end{array}\right)$$

Furthermore, let

$$P = ({\bf p}_{1}^{1} \cdots {\bf p}_{n_{1}}^{1} {\bf p}_{1}^{2} \cdots {\bf p}_{n_{2}}^{2} \cdots {\bf p}_{1}^{r} \cdots {\bf p}_{n_{r}}^{r}$$

Then $P$ is a regular matrix and satisfies

$$AP = P\left(\begin{array}{cccc} J(\lambda_{1},k_{1}^{1}) &&&\\ ... ...\\ & 0 & \ddots &\\ & & & J(\lambda_{r},k_{l_{r}}^{r}) \end{array}\right)$$

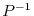Now multiply $P^{-1}$ from the left. Then we can obtain the required Jordan matrix $J = P^{-1}AP$. $\blacksquare$

Example 5..3  

Find the Jordan canonical form of the following matrix, and also the transition matrix $P$.

$$(1) \left(\begin{array}{ccc} 1&1&-1\\ 0&1&0\\ 0&0&1 \end{... ... \left(\begin{array}{ccc} 4&-3&3\\ -1&3&-2\\ -3&4&-3 \end{array}\right)$$

Answer (1) Find the eigenvalues of $A = \left(\begin{array}{ccc} 1&1&-1\\ 0&1&0\\ 0&0&1 \end{array}\right)$.

$$\Phi_{A}(\lambda) = A - \lambda I){\mathbf x} = (1 - \lambda)^{3} = 0$$

implies the eigenvalue of $A$ is 1 only. Then, $(A - I)$ is a nilpotent matrix and by the example 5.2, if we let

$$P = \left(\begin{array}{ccc} 1&0&0\\ 0&1&1\\ 0&0&1 \end{array}\right)$$

Then

$$P^{-1}AP = \left(\begin{array}{ccc} 1&1&0\\ 0&1&0\\ 0&0&1 \... ...ight) = \left(\begin{array}{cc} J(1,2) & 0\\ 0 & J(1,1) \end{array}\right)$$

(2) We find the eigenvalues of $A = \left(\begin{array}{ccc} 4&-3&3\\ -1&3&-2\\ -3&4&-3 \end{array}\right)$.

$$\Phi_{A}(\lambda) = A - \lambda I){\mathbf x} = (1 - \lambda)^{2}(2-\lambda) = 0$$

implies the eigenvalues of $A$ are 1 and 2. For the eigenvalue 1,

$$(A - 1I) = \left(\begin{array}{ccc} 3&-3&3\\ -1&2&-2\\ -3&4&... ... = \left(\begin{array}{ccc} 3&-3&3\\ -1&-1&1\\ -1&1&-1 \end{array}\right)$$

Thus,

$$W_{1}(1) \subset W_{2}(1) = W(2)$$

$$\dim W_{1}(1) = 1, \dim W_{2}(1) = 2$$

So,

$$W_{1}(1) = \{{\mathbf x} : (A - I){\mathbf x} = {\bf0}$$

implies ,

$$W_{1}(1) = <\left(\begin{array}{c} 0\\ 1\\ 1 \end{array}\right)>$$

$$W_{2}(1) = \{{\mathbf x} : (A - I)^{2}{\mathbf x} = {\bf0}$$

implies

$$W_{2}(1) = < {\mathbf x}, (A - I){\mathbf x}> = <\left(\begin{arr... ...end{array}\right) , \left(\begin{array}{c} 1\\ 1\\ 0 \end{array}\right)>$$

Next we find the eigenspace for the eigenvalue 2. Find

$$W_{1}(2) = (A - 2I){\mathbf x} = {\bf0}$$

Then

$$W_{1}(2) = W(2) = <\left(\begin{array}{c} 3\\ 1\\ -1 \end{array}\right)>$$

Now take ${\mathbf y} = \left(\begin{array}{c} 3\\ 1\\ -1 \end{array}\right)$. Let

$$P = ({\mathbf x} A{\mathbf x} {\mathbf y}) = \left(\begin{array}{ccc} 0&1&3\\ 1&1&1\\ 1&0&-1 \end{array}\right)$$

Then

$$P^{-1}AP = \left(\begin{array}{ccc} 1&1&0\\ 0&1&0\\ 0&0&2 \end{array}\right)$$

and this is Jordan canonical form of $A$.

Exercise5-2

1. Find the Jordan canonical from of the following nilpotent matrix and the transition matrix $P$. (a)

$$\ \ \left(\begin{array}{ccc} 0&2&1\\ 0&0&2\\ 0&0&0 \end{array}\right)$$

(a)

$$\left(\begin{array}{ccc} 0&-2&0\\ 0&0&0\\ 3&1&0 \end{array}\right)$$

2. Find the Jordan canonical form of the following matrix and the transition matrix $P$. (a)

$$\ \ \left(\begin{array}{ccc} 5&2&2\\ -2&0&-3\\ -1&-1&2 \end{array}\right)$$

(a)

$$\left(\begin{array}{ccc} 1&0&4\\ 2&-1&4\\ -1&-1&-5 \end{array}\right)$$