Nilpotent Matrix

$\spadesuit$ Generalized Eigenspace $\spadesuit$

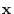Let $A$ be $n$ -square matrix and $W$ be a subspace of ${\mathcal C}^{n}$ . For any vector ${\mathbf x}$ in $W$ , if $A{\mathbf x} \in W$ , then the subspace $W$ is called an A - invariant.

We write the characteristic polynomial in terms of multiplicity of characteristeic values.

$\displaystyle \Phi_{A}(t) = (t - \lambda_{1})^{n_{1}}(t - \lambda_{2})^{n_{2}} \cdots (t - \lambda_{r})^{n_{r}}$

(5.1)

$\displaystyle \lambda_{i} \neq \lambda_{j} (i \neq j), n = n_{1}+n_{2}+\cdots+n_{r}$

Here, for the eigenvalues $\lambda_{i}(1 \leq i \leq r)$ , we let

$\displaystyle W(\lambda_{i}) = \{{\mathbf x} \in {\mathcal C}^{n} : (A - \lambda_{i}I )^{j} {\mathbf x} = {\bf0}\}$

Then the following holds.

$\displaystyle V(\lambda_{i}) = W_{1}(\lambda_{i}) \subset W_{2}(\lambda_{i}) \subset W_{3}(\lambda_{i}) \subset \cdots$

If you think of the dimension, this can not continue forever. Thus,

$\displaystyle W_{1}(\lambda_{i}) \subset W_{2}(\lambda_{i}) \subset \cdots \subset W_{l}(\lambda_{i}) = W_{l+1}(\lambda_{i}) = \cdots$

and $W(\lambda_{i}) = W_{l}(\lambda_{i})$ .

Theorem 5..1

Let

be the

th order square matrix and its characteristic polynomial be (5.1). Then for the generalized eigen space $W(\lambda_{i}) (1 \leq i \leq r)$ , the followings hold.

(1)	$W(\lambda_{i}) \bigcap W(\lambda_{j}) = {{\bf0}} (i \neq j)$
(2)	Generalized eigenvectors for different eigenvalues are linearly independent
(3)	$\dim W(\lambda_{i}) = n_{i}$

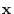Proof (1) For $i \neq j$ , there exists a vector ${\mathbf x}$ so that $W(\lambda_{i}) \bigcap W(\lambda_{j}) \ni {\mathbf x} \neq {\bf0}$ . Then there is a positive integer $k_{1}$ which satisfies

$\displaystyle (A - \lambda_{i}I)^{k_{1}} {\mathbf x} \neq {\bf0} \mbox{and} (A - \lambda_{i})^{k_{1}+1} {\mathbf x} = {\bf0}$

Let ${\mathbf y} = (A - \lambda_{i}I)^{k_{1}}{\mathbf x}$ . Then

$\displaystyle (A - \lambda_{i}I) {\mathbf y} = {\bf0}, W(\lambda_{i}) \bigcap W(\lambda_{j}) \ni {\mathbf y} \neq {\bf0}$

Since ${\mathbf y} \in W(\lambda_{j})$ , there is a positive integer $k_{2}$ which satisfies $(A - \lambda_{j}I)^{k_{2}} {\mathbf y} = {\bf0}$ . But $A{\mathbf y} = \lambda_{i}{\mathbf y}$ implies $(A - \lambda_{j}I)^{k_{2}}{\mathbf y} = (\lambda_{j}I - \lambda_{i}I)^{k_{2}}{\mathbf y} = {\bf0}$ . This contradicts the condition that for $i \neq j$ , $\lambda_{i} \neq \lambda_{j}$ .

(2) Let $\lambda_{1},\lambda_{2},\ldots,\lambda_{s}$ be the distinct eigenvalues of $A$ . Then for $W(\lambda_{i}) \ni {\mathbf x}_{i} \neq {\bf0}$ $(1 \leq i \leq s)$ , we show by induction that

$\displaystyle c_{1}{\mathbf x}_{1} + c_{2}{\mathbf x}_{2} + \cdots + c_{s}{\mathbf x}_{s} = {\bf0} \mbox{implies} c_{1} = c_{2} = \cdots = c_{s} = 0$

For

, it is obvious. We assume that

$\displaystyle c_{1}{\mathbf x}_{1} + c_{2}{\mathbf x}_{2} + \cdots + c_{s-1}{\mathbf x}_{s-1} = {\bf0} \mbox{implies } c_{1} = c_{2} = \cdots = c_{s-1} = 0$

Then by the condition,

$\displaystyle c_{1}{\mathbf x}_{1} + c_{2}{\mathbf x}_{2} + \cdots + c_{s}{\mathbf x}_{s} = {\bf0} **$

We multiply the integer $k$

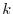, which satisfies $(A - \lambda_{s}I)^{k} {\mathbf x}_{s} = {\bf0}$ , to the equation (**) from the both sides.

$\displaystyle c_{1}(A - \lambda_{s}I)^{k}$		$\displaystyle {\mathbf x}_{1} + \cdots + c_{s-1}(A - \lambda_{s}I)^{k}{\mathbf x}_{s-1} + c_{s}(A - \lambda_{s}I)^{k}{\mathbf x}_{s}$
	$\displaystyle =$	$\displaystyle c_{1}(A - \lambda_{s}I)^{k}{\mathbf x}_{1} + \cdots + c_{s-1}(A - \lambda_{s}I)^{k}{\mathbf x}_{s-1} = {\bf0}$

Since $W(\lambda_{i})$ is $(A - \lambda_{s}I)$ -invariant, $(A - \lambda_{s}I)^{k}{\mathbf x}_{i} \in W(\lambda_{i})$ . Also, from (1), for $i \neq s$ , ${\mathbf x}_{i} \not\in W(\lambda_{s})$ . Thus, $(A - \lambda_{s}I)^{k}{\mathbf x}_{i} \neq {\bf0}$ $(1 \leq i \leq s-1)$ . Then by the induction hypothesis, $c_{i} = 0 (1 \leq i \leq s-1)$ . Therefore, $c_{s}{\mathbf x}_{s} = {\bf0}$ and we have $c_{s} = 0$ .

(3) by the linearly independence shown (2), we have

$\displaystyle \dim W(\lambda_{1}) + \cdots + \dim W(\lambda_{r}) \leq n$

Also, $n = n_{1} + n_{2} + \cdots + n_{r}$ . So, to show (3), it is enough to show $n_{i} \leq \dim W(\lambda_{i})$ $(1 \leq i \leq r)$ い.

The matrix $A$ can be transformed to the following triangular matrix by using unitary matrix $U$ .

$\displaystyle U^{-1}AU = \left(\begin{array}{rrrrrrrrrr} \lambda_{1}&&&&&&&&&\\... ...&&&\lambda_{r}&&\\ &&&&&&&&\ddots&\\ &&&&&&&&&\lambda_{r} \end{array}\right)$

Now, we let

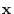$\displaystyle V_{i} = \left\{{\mathbf x} = \left(\begin{array}{c} x_{1}\\ x_... ...ray}\right) \in {\mathcal C}^{n} : x_{i} = 0 (n_{1}+1 \leq i \leq n) \right\}$

Then $V_{1}$ is $n_{1}$ th vector subspace of ${\mathcal C}^{n}$ . Also, $B = U^{-1}AU$ implies for every vector ${\mathbf x}$ of $V_{1}$ , we have

$\displaystyle (B - \lambda_{1}I)^{n_{1}}{\mathbf x} = U^{-1}(A - \lambda_{1}I)^{n_{1}}U{\mathbf x} = {\bf0}$

Note that

is regular,

$\displaystyle (A - \lambda_{1}I)^{n_{1}} U{\mathbf x} - {\bf0}$

Therefore, let $V_{2} = \{U{\mathbf x} : x \in V_{1}\}$ . Then $V_{2}$ is $n_{1}$ subspace included in $W(\lambda_{1})$ and obtain the inequality $n_{1} \leq \dim W(\lambda_{1})$ . Now switching the order of eigenvalues, we have $n_{i} \leq \dim W(\lambda_{i})$ $(1 \leq i \leq r)$ . $\blacksquare$

Theorem 5..2

Let

be the

th square matrix and its characteristic polynomial be (*). Then $A$

an be transformed by $P$

to the followings.

$\displaystyle P^{-1}AP = \left(\begin{array}{cccc} A_{1} &&&\\ &A_{2}&&\\ &&&\ddots\\ &&&A_{r} \end{array}\right)$

Note that $A_{i}(1 \leq i \leq r)$ is $n_{i}$ th square matrix and its characteristic polynomial is $\Phi_{A}(t) = (t - \lambda_{i})^{n_{i}}$ .

Proof From $W(\lambda_{i})$ , we take the basis ${\bf p}_{1}^{i}, \ldots,{\bf p}_{n_{i}}^{i}$ . Since $W(\lambda_{i})$ is $A$ -invariant, we have

$\displaystyle A{\bf p}_{j}^{i} = a_{1j}^{i}{\vert bf p}_{1}^{i} + \cdots + a_{n_{i}j}^{i}{\bf p}_{n_{i}}^{i} (1 \leq j \leq n_{i})$

Now let $A_{i} = (a_{jk}^{i})$ . Then $A_{i}$ is $n_{i}$ th square matrix. By the theorem 5.1,

$\displaystyle \{{\bf p}_{1}^{1},\ldots,{\bf p}_{n_{1}}^{1},{\bf p}_{1}^{2},\ldots,{\bf p}_{n_{2}}^{2},\ldots,{\bf p}_{1}^{r},\ldots,{\bf p}_{n_{r}}^{r}\}$

is the basis of ${\mathcal C}^{n}$ . Therefore, we let

$\displaystyle P = ({\bf p}_{1}^{1} \cdots {\bf p}_{n_{1}}^{1} {\bf p}_{1}^{2} \cdots {\bf p}_{n_{2}}^{2} \cdots {\bf p}_{1}^{r} \cdots {\bf p}_{n_{r}}^{r})$

Then

is a regular matrix and

$\displaystyle AP = P\left(\begin{array}{cccc} A_{1} &&&\\ &A_{2}&0&\\ &&&\ddots\\ &&0&A_{r} \end{array}\right)$

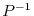Multiply both sides by $P^{-1}$ , we obtain the required equation.

Using this relation,

$\displaystyle \Phi_{A}(t)$	$\displaystyle =$	$\displaystyle \Phi_{P^{-1}AP}(t) = (t - \lambda_{1})^{n_{1}}(t - \lambda_{2})^{n_{2}}\cdots(t - \lambda_{r})^{n_{r}}$
	$\displaystyle =$	$\displaystyle \Phi_{A_{1}}(t)\Phi_{A_{2}}(t) \cdots \Phi_{A_{r}}(t)$

Therefore, if we can show that the eigenvalue of $A_{i}$ is $\lambda_{i}$ only. Then we can show

$\displaystyle \Phi_{A_{i}}(t) = (t - \lambda_{i})^{n_{i}}$

and $A_{i}$ has the eigenvalues $\lambda_{i}(j \neq i)$ and the eigenvector corresponds to $\lambda_{i}$ are

$\displaystyle {\mathbf x} = \left(\begin{array}{c} x_{1}\\ x_{2}\\ \vdots\... ...}\right) = \left(\begin{array}{c} 0\\ 0\\ \vdots\\ 0 \end{array}\right)$

In other words, if $A_{i}{\mathbf x} = \lambda_{j}{\mathbf x}$ and let

$\displaystyle {\mathbf {\bar{x}}} = \left(\begin{array}{c} 0\\ \vdots\\ 0\... ... \\ \\ \end{array}\right\} & n_{i+1} + \cdots + n_{r} \end{array}\right.$

Then ${\mathbf {\bar x}} \neq {\bf0}$ で $P^{-1}AP{\mathbf {\bar x}} = \lambda_{j}{\mathbf {\bar x}}$ . Therefore,

$\displaystyle {\bf0} \neq P{\mathbf {\bar x}} = x_{1}{\bf p}_{1}^{i} + \cdots + x_{n_{i}}{\bf p}_{n_{i}}^{i} \in W(\lambda_{i})$

satisfies $AP{\mathbf {\bar x}} = \lambda_{j}P{\mathbf {\bar x}}$ . In other words, it satisfies $(A - \lambda_{j}I)P{\mathbf {\bar x}} = {\bf0}$ . But then this means that $P{\mathbf {\bar x}} \in W(\lambda_{j})$ and this contradicts the theorem 5.1. $\blacksquare$