Normal Matrix

In this section, we study the square matrix which is diagonalizable.

Suppose that $n$ -square matrix $A$ is transposed to a diagonal matrix $U^{*}AU = D$ by an unitary matrix $U$ . Here $D$ is a diagonal matrix so that $D^{*}D = DD^{*}$ . Also since $A = UDU^{*}$ , we have

$\displaystyle A^{*}A = (UD^{*}U^{*})(UDU^{*}) = UDD^{*}U^{*} ,$

$\displaystyle AA^{*} = (UDU^{*})(UD^{*}U^{*}) = UDD^{*}U^{*} .$

Thus, $A^{*}A = AA^{*}$ . In other words, The square matrix $A$

which is tranposed to diagonal matrix by an unitary matrix satisfies $AA^{*} = A^{*}A$ . Then we call this matrix normal matrix

Conversely, suppose that $A$ is a normal matrix. Then by the theorem 4.1, using the unitary matrix $U$ , we have

$\displaystyle U^{-1}AU = U^{*}AU = \left(\begin{array}{rrrr} \lambda_{1}&b_{12}... ...n}\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\lambda_{n} \end{array}\right)$

Let this upper triangular matrix be $S$

. Then

$\displaystyle S^{*} = U^{*}A^{*}U = \left(\begin{array}{rrrr} \bar{\lambda_{1}}... ...vdots\\ \bar{b_{1n}}&\bar{b_{2n}}&\cdots&\bar{\lambda_{n}} \end{array}\right)$

Since $AA^{*} = A^{*}A$ , we have

$\displaystyle S^{*}S = (U^{*}A^{*}U)(U^{*}AU) = U^{*}A^{*}AU = U^{*}AA^{*}U = (U^{*}AU)(U^{*}A^{*}U) = SS^{*}.$

Rewrite this by using matrices, we have

$\displaystyle S^{*}S$	$\displaystyle =$	$\displaystyle \left(\begin{array}{rrrr} \bar{\lambda_{1}}&0&\cdots&0\\ \bar{b_... ...2n}\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\lambda_{n} \end{array}\right)$
	$\displaystyle =$	$\displaystyle \left(\begin{array}{rrrr} \lambda_{1}&b_{12}&\cdots&b_{1n}\\ 0&\... ... \bar{b_{1n}}&\bar{b_{2n}}&\cdots&\bar{\lambda_{n}} \end{array}\right) = SS^{*}$

Now we check to see the diagonal ecomponents. Compare the $(1,1)$ component.

$\displaystyle \lambda_{1}\bar{\lambda_{1}}+b_{12}\bar{b_{12}}+\cdots+b_{1n}\bar{b_{1n}} = \bar{\lambda_{1}}\lambda_{1}$

Then,

$\displaystyle b_{12} = b_{13} = \cdots = b_{1n} = 0$

Compare

component. Using $b_{12} = 0$ , we have

$\displaystyle \lambda_{2}\bar{\lambda_{2}}+b_{23}\bar{b_{23}}+\cdots+b_{2n}\bar{b_{2n}} = \bar{\lambda_{2}}\lambda_{2}$

Thus,

$\displaystyle b_{23} = b_{24} = \cdots = b_{2n} = 0$

Similarly for the rest, we can show $b_{ij} = 0 (i < j)$ . Thus, $U^{-1}AU$ is a diagonal matrix. Putting together, we have the following theorem.

Theorem 4..5

For

-square matrix $A$

, the following conditions are equivalent.
$(1)$

is diagonalizable by some unitary matrix $U$

is normal.

Now we know that the normal matrix is diagonalizable by an unitary matrix. The normal matrix is a matrix which is commutative of the product of the matrix itself and the conjugate transpose of the matrix. Thus, Hermite matrix, unitary matrix are normal matrix.

Definition 4..1

For any basis ${\bf v}_{1},{\bf v}_{2}$ of the complex vector space $V$

, if real numbers $({\bf v}_{1}, {\bf v}_{2})$ are defined and it has the following properties, then we say $({\bf v}_{1}, {\bf v}_{2})$ is an inner product of ${\bf v}_{1}$ and ${\bf v}_{2}$ .

For any vectors ${\bf v}, {\bf v}_{1},{\bf v}_{2},{\bf v}_{3}$ in a complex vector space and any complex numbers $\alpha, \beta$ , the followings are satisfied.
$1.$ $(\alpha {\bf v}_{1} + \beta {\bf v}_{2},{\bf v}_{3}) = \alpha ({\bf v}_{1},{\bf v}_{3}) + \beta ({\bf v}_{2},{\bf v}_{3})$
$2.$ $({\bf v}_{1},{\bf v}_{2}) = \overline{({\bf v}_{2},{\bf v}_{1})}$
$3.$ $({\bf v},{\bf v}) \geq 0, ({\bf v},{\bf v}) = 0$ and ${\bf v} = {\bf0}$ are equivalent.

Example 4..4

Show that a Hermitian matrix is a normal matrix. Find all eigenvalues.

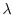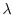Answer Let $A$ be the Hermitian matrix. Then since $A = A^{*}$ , we have $AA^{*} = A^{*}A$ . Thus, $A$ is a normal matrix. Next let $\lambda$ be the eigenvalue of $A$ and ${\bf a}$ be the eigenvector of $A$ corresponding to $\lambda$ . Then by the definition4.2,

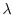$\displaystyle \lambda ({\bf a},{\bf a})$	$\displaystyle =$	$\displaystyle (\lambda {\bf a},{\bf a}) = (A{\bf a},{\bf a}) = ({\bf a},{\bf A^{*}}{\bf a})$
	$\displaystyle =$	$\displaystyle ({\bf a},A{\bf a}) = ({\bf a},\lambda {\bf a}) = \bar{\lambda}({\bf a},{\bf a})$

Thus, $\lambda = \bar{\lambda}$ . hence, $\lambda$ is real number. $\blacksquare$

From this example, you can see that if $A$ is a Hermitial matrix, the diagonanl components of the transposed matrix $U^{-1}AU$ are real numbers. Furthermore, if $A$ is a real square matrix, the following theorem holds.

Theorem 4..6

For real

-square matrix $A$

, the following conditions are equivalent.
$(1)$

is an orthogonal matrix and diagonalizable.
$(2)$

is a real symmetric matrix.

$\spadesuit$ Quadratic Form $\spadesuit$

For any $n$ -squar real matrix $A$ and vectors ${\mathbf x},{\mathbf y} \in {\mathcal R}^{n}$ , the expression

$\displaystyle A({\mathbf x},{\mathbf y})$	$\displaystyle =$	$\displaystyle {\mathbf x}^{t}A{\mathbf y} = (x_{1},x_{2},\ldots,x_{n})\left(\be... ...ght)\left(\begin{array}{r} y_{1}\\ y_{2}\\ \vdots\\ y_{n} \end{array}\right)$
	$\displaystyle =$	$\displaystyle \sum_{i,j=1}^{n}a_{ij}x_{i}y_{j} = a_{11}x_{1}y_{1} + a_{12}x_{1}y_{2} + \cdots + a_{nn}x_{n}y_{n}$

is called a bilinear form of $A$

Also, for any $n$ -square real symmetric matrix $A$ and ${\mathbf x} = {\mathbf y}$ , the expression

$\displaystyle A({\mathbf x},{\mathbf x})$	$\displaystyle =$	$\displaystyle {\mathbf x}^{t}A{\mathbf x} = (x_{1},x_{2},\ldots,x_{n})\left(\be... ...ght)\left(\begin{array}{r} x_{1}\\ x_{2}\\ \vdots\\ x_{n} \end{array}\right)$
	$\displaystyle =$	$\displaystyle a_{11}x_{1}^{2} + a_{22}x_{2}^{2} + \cdots + a_{nn}x_{n}^{2} + 2\sum_{i<j}a_{ij}x_{i}x_{j}$

is called a quadratic form of $A$

Example 4..5

Show $x_{1}^2 + x_{2}^2 -2x_{1}x_{2} + 4x_{1}x_{3} - 4x_{2}x_{3}$ using a matrix. a

Answer Since $a_{11} = a_{22} = a_{12} = a_{21} = 1, a_{13} = a_{31} = 2, a_{23} = a_{32} = -2, a_{33} = 0$ ,

$\displaystyle (x_{1},x_{2},x_{3})\left(\begin{array}{rrr} 1&1&2\\ 1&1&-2\\ 2&... ...array}\right)\left(\begin{array}{r} x_{1}\\ x_{2}\\ x_{3} \end{array}\right)$

$\blacksquare$

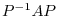Suppose that a matrix $A$ is real symmetric. Then by the theorem4.2, $A$ is diagonalizable by the orthogonal matrix. So, let $P$ be the orthogonal matrix so that $P^{-1}AP$ is diagonalizable. Now set ${\mathbf x} = P{\mathbf y}$ . Then

$\displaystyle {\mathbf x}^{t}A{\mathbf x} = {\mathbf y}^{t}(P^{t}AP){\mathbf y}$	$\displaystyle =$	$\displaystyle (y_{1},\ldots,y_{n})\left(\begin{array}{rrr} \lambda_{1}&\cdots&0... ...array}\right)\left(\begin{array}{r} y_{1}\\ \vdots\\ y_{n} \end{array}\right)$
	$\displaystyle =$	$\displaystyle \lambda_{1}y_{1}^{2} + \lambda_{2}y_{2}^{2} + \cdots + \lambda_{n}y_{n}^{2}$

This shows the following theorem.

Theorem 4..7

A real bilinear matrix ${\mathbf x}^{t}A{\mathbf x}$ can be tranposed to standard form

$\displaystyle {\mathbf x}^{t}A{\mathbf x} = {\mathbf y}^{t}(P^{t}AP){\mathbf y} = \lambda_{1}y_{1}^{2} + \lambda_{2}y_{2}^{2} + \cdots + \lambda_{n}y_{n}^{2}$

by ${\mathbf x} = P{\mathbf y}$ . Here, $\lambda_{i} (i = 1,2,\ldots,n)$ are eigenvalues of $A$

From this, we see the followings:
$(1)$ A real symmetric bilinear form $f$ is said to be positive definite if eigenvalues of $A$ are all positive and for any ${\mathbf x} \neq 0$ , ${\mathbf x}^{t}A{\mathbf x} > 0$ .
$(2)$ A real symmetric bilinear form $f$ is said to be negative definite if eigenvalues of $A$ are all netative and for any ${\mathbf x} \neq 0$ , ${\mathbf x}^{t}A{\mathbf x} < 0$ .

Example 4..6

Express a real bilinear form $A({\mathbf x},{\mathbf x}) = x_{1}^{2} + x_{2}^{2} + x_{3}^{2} + 4x_{1}x_{2} + 4x_{2}x_{3} + 4x_{3}x_{1}$ using a matrix. Determine whether the matrix $A$

is positive definite. Find the standard bilinear form.

Answer The matrix for the bilinear form is

$\displaystyle A = \left(\begin{array}{rrr} 1&2&2\\ 2&1&2\\ 2&2&1 \end{array}\right)$

Then since $\Phi_{A}(t) = \det(A - tI) = -(t+1)^{2}(t-5)$ , the eigenvector of $A$

are

(multiplicity 2), $5$

. Thus, the bilinear form is not positive definite. Since $A$

is a real symmetric matrix, we can find the orthogonal matrix $P$

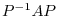sothat $P^{-1}AP$ is a diagonal matrix. Thus by putting ${\mathbf x} = P{\mathbf y}$ . then we have the standard bilinear form.

$\displaystyle {\mathbf x}^{t}A{\mathbf x} = -y_{1}^{2} - y_{2}^{2} + 5y_{3}^{2}$

$\blacksquare$

Example 4..7

Express $A({\mathbf x},{\mathbf x}) = x_{1}^{2} + 5x_{2}^{2} + 8x_{3}^{2} + 4x_{1}x_{2} - 8x_{2}x_{3} - 6x_{3}x_{1}$ using a matrix. Find the standard bilinear form.

Answer The matrix for this bilinear form is

$\displaystyle A = \left(\begin{array}{rrr} 1&2&-3\\ 2&5&-4\\ -3&-4&8 \end{array}\right)$

Note that $\Phi_{A}(t) = \det(A - tI) = -t^3 + 14t^2 - 24t - 5$ . Then we can not find the eigenvalues of $A$

easily. So, we need a way to find the standard bilinear form without knowing eigenvalues.

Remember the regular matrix is a product of elementary matrices. So, to diagonalize, we can use the elementary operations.

$\displaystyle A = \left(\begin{array}{rrr} 1&2&-3\\ 2&5&-4\\ -3&-4&8 \end{array}\right)$

implies that $A$

is a symmetric matrix. Then we apply $-2R_{1} + R_{2}$ to the $R_{2}$ and $3R_{1}+R_{3}$ to the $R_{3}$ . Next we apply $-2R_{2} + R_{3}$ to the $R_{3}$ . Then we have

$\displaystyle [A:I]$	$\displaystyle =$	$\displaystyle \left(\begin{array}{rrrrrr} \!\!1&\!\!2&\!\!-3&1&0&0\\ \!\!2&\!\... ...-3&\!\!1&0&0\\ 0&1&\!\!2&\!\!-2&1&0\\ 0&2&\!\!-1&\!\!3&0&1 \end{array}\right)$
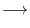	$\displaystyle \longrightarrow$	$\displaystyle \left(\begin{array}{rrrrrr} 1&2&-3&1&0&0\\ 0&1&2&-2&1&0\\ 0&0&-5&7&-2&1 \end{array}\right) = B.$

Next we apply the same elementary operation on $R_{2}, R_{3}$ to the columns $C_{2}, C_{3}$ . Then we have

$\displaystyle B$	$\displaystyle =$	$\displaystyle \left(\begin{array}{rrrrrr} 1&0&0&1&0&0\\ 0&1&2&-2&1&0\\ 0&0&-5&7&-2&1 \end{array}\right)$
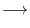	$\displaystyle \longrightarrow$	$\displaystyle \left(\begin{array}{rrrrrr} 1&0&0&1&0&0\\ 0&1&0&-2&1&0\\ 0&0&-5&7&-2&1 \end{array}\right).$

As a result, $A$

is a diagonalized matrix. Let $P^{t} = \left(\begin{array}{rrr} 1&0&0\\ -2&1&0\\ 7&-2&1 \end{array}\right)$ . Then

$\displaystyle P^{t}AP = \left(\begin{array}{rrr} 1&0&0\\ 0&1&0\\ 0&0&-5 \end{array}\right)$

. Thus,

$\displaystyle {\mathbf x}^{t}A{\mathbf x}$	$\displaystyle =$	$\displaystyle {\mathbf y}^{t}(P^{t}AP){\mathbf y} = {\mathbf y}^{t}\left(\begin{array}{rrr} 1&0&0\\ 0&1&0\\ 0&0&-5 \end{array}\right){\mathbf y}$
	$\displaystyle =$	$\displaystyle y_{1}^2 + y_{2}^2 - 5y_{3}^2 . \ensuremath{ \blacksquare}$

If $A$ is a complex square matrix, we can do the same thing as for a real square matrix.

Given any $n$ -square complex matrix $A$ and any vectors ${\mathbf x},{\mathbf y} \in { C}^{n}$ ,

$\displaystyle A({\mathbf x},{\mathbf y})$	$\displaystyle =$	$\displaystyle {\mathbf x}^{*}A{\mathbf y} = (\bar{x_{1}},\bar{x_{2}},\ldots,\ba... ...ght)\left(\begin{array}{r} y_{1}\\ y_{2}\\ \vdots\\ y_{n} \end{array}\right)$
	$\displaystyle =$	$\displaystyle \sum_{i,j=1}^{n}a_{ij}\bar{x_{i}}y_{j}$
	$\displaystyle =$	$\displaystyle a_{11}\bar{x_{1}}y_{1} + a_{12}\bar{x_{1}}y_{2} + \cdots + a_{nn}\bar{x_{n}}y_{n}$

is called a Hermitian form of $A$

Suppose that $A$ is a Hermitian matrix of the order $n$ and ${\mathbf x} = {\mathbf y}$ . Then

$\displaystyle A({\mathbf x},{\mathbf x})$	$\displaystyle =$	$\displaystyle {\mathbf x}^{*}A{\mathbf x} = (\bar{x_{1}},\bar{x_{2}},\ldots,\ba... ...ght)\left(\begin{array}{r} x_{1}\\ x_{2}\\ \vdots\\ x_{n} \end{array}\right)$
	$\displaystyle =$	$\displaystyle a_{11}\bar{x_{1}}{x_{1}} + a_{22}\bar{x_{2}}{x_{2}} + \cdots + a_{nn}\bar{x_{n}}{x_{n}} + 2\sum_{i<j}a_{ij}\bar{x_{i}}x_{j}$

is said to be complex quadratic form of $A$

. In this case, $A$

is a Hermitian matrix, that is normal matrix. By the theorem 4.2, $A$

is diagonalizable by unitary matrix. Then choose the unitary matrix $U$

so that $U^{-1}AU$ is diagonal matrix. Now let ${\mathbf x} = U{\mathbf y}$ . Then we have

$\displaystyle {\mathbf x}^{}A{\mathbf x} = {\mathbf y}^{}(U^{*}AU){\mathbf y}$	$\displaystyle =$	$\displaystyle (\bar{y_{1}},\ldots,\bar{y_{n}})\left(\begin{array}{rrr} \lambda_... ...array}\right)\left(\begin{array}{r} y_{1}\\ \vdots\\ y_{n} \end{array}\right)$
	$\displaystyle =$	$\displaystyle \lambda_{1}\bar{y_{1}}{y_{1}} + \lambda_{2}\bar{y_{2}}{y_{2}} + \cdots + \lambda_{n}\bar{y_{n}}{y_{n}}$

This proves the next theorem.

Theorem 4..8

A complex bilinear form ${\mathbf x}^{*}A{\mathbf x}$ can be transformed to the standard form by the appropiate transformation ${\mathbf x} = U{\mathbf y}$ by the unitary matrix $U$

$\displaystyle {\mathbf x}^{*}A{\mathbf x} = {\mathbf y}^{*}(U^{*}AU){\mathbf y}... ..._{1}} + \lambda_{2}\bar{y_{2}}{y_{2}} + \cdots + \lambda_{n}\bar{y_{n}}{y_{n}}$

Here, $\lambda_{i} (i = 1,2,\ldots,n)$ are eigenvalues of $A$

Exercise4-4

1. Find the unitary matrix $U$ so that $U^{-1}AU$ is diagonal.

$\displaystyle A = \left(\begin{array}{cc} 1&1-i\\ 1+i&2 \end{array}\right)$

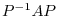2. Find the orthogonal matrix $P$ so that $P^{-1}AP$ is diagonal.

$\displaystyle A = \left(\begin{array}{rrr} 1&0&-1\\ 0&-1&0\\ -1&0&1 \end{array}\right)$

3. Find a condition so that $A = \left(\begin{array}{rr} 0&a_{1}\\ a_{2}&0 \end{array}\right)$ can be transformed to diagonal matrix by the unitary matrix.

4. Find the orthogonal matrix so that the following bilinear form becomes the standard form.

$\displaystyle x_{1}^2 + 2x_{2}^{2} - 3x_{3}^{2} + 2x_{1}x_{2}$

5. Standarize the following Hermite matrix by using unitary matrix.

$\displaystyle x_{1}\bar{x_{1}} + (1 - i)x_{1}\bar{x_{2}} + (1 + i)x_{2}\bar{x_{1}} + 2x_{2}\bar{x_{2}}$