Next: Matrix Transformation and Eigen Up: Linear Mapping Previous: Linear Mapping Contents Index
 Mapping
Mapping

In chapter 1 and chapter 2, we have studied about vector spaces. In this chapter, we study the relationship between two vector spaces. Before going to detail, we review about the mapping.
Consider two vector spaces  and
and  . For any element
. For any element  of
of  , there is assigned a unique element
, there is assigned a unique element  of
of  ; the collection,
; the collection,  , of such assignments is called a mapping from
, of such assignments is called a mapping from  to
to  , and is written
, and is written

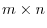 matrix represents a mapping which maps a
matrix represents a mapping which maps a  th column vector to
th column vector to 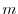 th column vector. In other words, it is a mapping from
th column vector. In other words, it is a mapping from
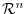 to
to
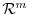 .
.
 Linear Mapping
Linear Mapping

In vector space, an addition and a scalar product are defined. So, a mapping between two vector spaces had better to satisfy an addition and scalar product.
 be vector spaces. Then the mapping
be vector spaces. Then the mapping
 is called a linear mapping if it satisfies the following two conditions.
is called a linear mapping if it satisfies the following two conditions.


 , We say the mapping
, We say the mapping  is a linear transformation of
is a linear transformation of  .
.
A linear mapping from  to
to  is a mapping which preserves the properties of vector space.
The image of
is a mapping which preserves the properties of vector space.
The image of  , written
, written  , is the set of image point in
, is the set of image point in  :
:

 , written
, written
 , is the set of elements in
, is the set of elements in  which map into
which map into  :
:

The following theorems is easily proven.
 be a linear mapping. Then the image of
be a linear mapping. Then the image of  is a subspace of
is a subspace of  and the kernel of
and the kernel of  is a subspace of
is a subspace of  .
.
 be the matrix with
be the matrix with
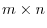 . Let
. Let

 . Then show that
. Then show that  is a linear mapping.
is a linear mapping.
Answer
For any vectors
 and any real number
and any real number  , we have
, we have


 is a linear mapping.
is a linear mapping.

Suppose that the linear mapping
 satisfies the following condition:
satisfies the following condition:

 is called a one-to-one or injective.
is called a one-to-one or injective.
If a linear mapping
 satisfies
satisfies  , then
, then  is called onto mapping from
is called onto mapping from  to
to  or surjective.
or surjective.
 are linear mappings. Then show that the compostion mapping
are linear mappings. Then show that the compostion mapping  is a linear mapping.
is a linear mapping.
Answer
 |
 |
 |
|
 |
 |
||
 |
 |
 is a linear mapping..
is a linear mapping..

 Isomorphic Mapping
Isomorphic Mapping

One-to-one and onto mapping is called an isomorphism. If there is an isomorphism from vector space  to
to  , Then we say
, Then we say  and
and  are isomorphic and denoted by
are isomorphic and denoted by  . If
. If
 is isomorphic and
is isomorphic and
 , then set
, then set
 . Then we can find a mapping from
. Then we can find a mapping from  to
to  . This mapping is called an inverse mapping and denoted by
. This mapping is called an inverse mapping and denoted by
 .
.
 be a linear mapping. Then the following conditions are equivalent.
be a linear mapping. Then the following conditions are equivalent.



 is isomorphic. In other wordsm
is isomorphic. In other wordsm




 is isomorphic.
is isomorphic.
 If
If
 is the basis of
is the basis of
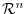 then the set of images of
then the set of images of  :
:
 は
は  is the basis of
is the basis of  .
.
Proof

Let the basis of  be
be
 and
and
 be the basis of
be the basis of
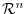 . Now define
. Now define
 as
as
 . Then
. Then  is a linear mapping (Excercise3.1). Also let
is a linear mapping (Excercise3.1). Also let
 . Then for some
. Then for some
 , we have
, we have


 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
 is injective.
Next suppose that
is injective.
Next suppose that
 . Then
. Then
 . This shows that
. This shows that
 is the image of
is the image of  . Thus,
. Thus,
 is injective. Therefore a linear mapping
is injective. Therefore a linear mapping  is bijective. This shows tha t
is bijective. This shows tha t  is isomorphism.
is isomorphism.

 . Then
. Then
 . By the assumption.
. By the assumption.
 . Thus,
. Thus,
 . Since
. Since  is bijection, we have
is bijection, we have
 .
.

 is isomorphi, for any
is isomorphi, for any
 , we have
, we have
 . and
. and
 exist. By the linearlity of
exist. By the linearlity of  , we have
, we have


 is bijection. First of all, we show
is bijection. First of all, we show
 implies that
implies that
 .
.

 implies that
implies that

 is isomorphic.
is isomorphic.

 is the basis of
is the basis of  , it is enough to show this set is linearly indepenent and the vector space spanned by this set is
, it is enough to show this set is linearly indepenent and the vector space spanned by this set is  .
.


 is isomorphic. Then
is isomorphic. Then

 is linearly independent. Thus, we have
is linearly independent. Thus, we have
 . Hence,
. Hence,

 . Then
. Then

 .
.

 is basis of
is basis of  . Thus,
. Thus,
 .
.

 Matrix Representation
Matrix Representation

To check a linear mapping of the finite dimensional vector space, we apply a matrix for the linear mapping. Then the properties of the linear mapping can be seen directly as the properties of matrices.
For example, consider the linear mapping  which describes the rotation of the point on
which describes the rotation of the point on  plane with
plane with  rotation to a point
rotation to a point  .
Consider the basis of
.
Consider the basis of  ,
,
 .
Then
.
Then

 |
 |
 |
|
 |
 |

 . Let
. Let

 . Let
. Let
 and the image of
and the image of  be
be



 , we have
, we have
 |
 |
 |
|
 |
 |
 is in
is in
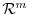 , we can express as
, we can express as

 |
 |
 |
|
 |
 |
||
 |
 |
||
 |
 |
 is the basis of
is the basis of
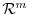 . Then the corresponding coefficients must be equal. So, we have the following relations:
. Then the corresponding coefficients must be equal. So, we have the following relations:

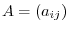 . This matrix
. This matrix  is called a matrix representation of
is called a matrix representation of  on the basis
on the basis

![$[T]_{¥bf v}^{¥bf w}$](img1147.png) . For
. For  , we take the basis of
, we take the basis of
 of
of  and the basis
and the basis
 of
of  to be the same and write
to be the same and write
![$[T]_{¥bf v}$](img1149.png) . Also for
. Also for
 , the following usual basis
, the following usual basis

 is given by
is given by
![$[T]_{¥bf e}$](img1152.png) or
or ![$[T]$](img1153.png) To summarize,
A linear mapping
To summarize,
A linear mapping  from
from
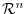 to
to
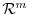 is represented by the
is represented by the
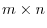 matrix which shows the image of the basis of
matrix which shows the image of the basis of
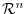 by the basis of
by the basis of
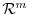 . Then it satisfies
. Then it satisfies
![$¥displaystyle [T({¥mathbf x})]_{¥bf w} = [T]_{¥bf v}^{¥bf w}[{¥mathbf x}]_{¥bf v} $](img1154.png)
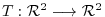 be given by
be given by
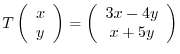 . Find the matrix representation
. Find the matrix representation ![$[T]$](img1153.png) of
of  relative to the basis
relative to the basis
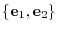 and the matrix representation of
and the matrix representation of ![$[T]_{w}$](img1158.png) relative to the basis
relative to the basis
 . Furthermore, find the matrix representation
. Furthermore, find the matrix representation
![$[T]_{¥bf e}^{¥bf w}$](img1160.png) of
of  relative to
relative to
 .
.
Answer

![$[T] = ¥left(¥begin{array}{cc}
3&-4¥¥
1&5
¥end{array}¥right)$](img1163.png) .
.
 |
 |
 |
|
 |
 |
 |
 implies that
implies that
 . Thus,
. Thus,
![$[T]_{¥bf w} = ¥left(¥begin{array}{cc}
77&124¥¥
-43&-69
¥end{array}¥right)$](img1170.png) .
.
 |
 |
 |
|
 |
 |
 |
![$[T]_{¥bf e}^{¥bf w} = ¥left(¥begin{array}{cc}
-13&30¥¥
8&-17
¥end{array}¥right)$](img1175.png) .
.

Let  be a linear mapping
be a linear mapping
 . Then
. Then  is a set of all elements of
is a set of all elements of
 so that the image of
so that the image of  is
is  . In other words, it is the same as the solution space of the system of linear equations.
. In other words, it is the same as the solution space of the system of linear equations.


 .
.  is the set all images of elements in
is the set all images of elements in
 . Then
. Then
 . From this, we have the following theorem.
. From this, we have the following theorem.
 be a linear mapping. Then the following is true.
be a linear mapping. Then the following is true.

 by
by
 . Find the
. Find the
 .
.
Answer
Since
 is the same as
is the same as
 . Also,
. Also,
 . Thus if we find the
. Thus if we find the
 , then we can find
, then we can find
 .
.

 . Thus
. Thus
 .
.

Given vector spaces
 , there is a linear mapping
, there is a linear mapping  such that
such that

 is also linear mapping. (see Example3.1). Then take basis for each vector space and let the matrix representation for linear mappings
is also linear mapping. (see Example3.1). Then take basis for each vector space and let the matrix representation for linear mappings  be
be 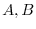 . Then for
. Then for
 , we have
, we have

 is
is  .
.
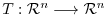 relative to the basis
relative to the basis
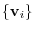 be
be  . Then the followings areequivalent.
. Then the followings areequivalent.

 is isomorphic.
is isomorphic.
 The matrix
The matrix  is regular.
is regular.
Proof

Let the matrix representation of
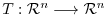 be
be  . Since
. Since  is isomorphic,
is isomorphic,  exists. Now let the matrix representation of
exists. Now let the matrix representation of  be
be  . Then
. Then  and
and  is regular.
is regular.

Suppose that  is regular. Then there is a matrix
is regular. Then there is a matrix  such that
such that  . Now let
. Now let  be the linear mapping on
be the linear mapping on  . Then
. Then
 . Thus, by Exercise 3.1,
. Thus, by Exercise 3.1,  is isomorphic.
is isomorphic.

1. Determine whether the following mapping is linear mapping.


2. Let  be the
be the  dimensional vector space. Let
dimensional vector space. Let
 be the basis of
be the basis of  . Define
. Define
 by
by
 . Then show that
. Then show that  is a linear mapping.
is a linear mapping.
3. Let
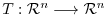 be a linear mapping. Then the followings are equivalent.
be a linear mapping. Then the followings are equivalent.
 is isomorphic.
is isomorphic.
 such that
such that
 and
and
 .
.
4. Suppose that
 is a linear mapping. Show that
is a linear mapping. Show that
 are the subspace of
are the subspace of  .
.
5. Let
 be a linear transformation such that
be a linear transformation such that
 . Find the matrix representation
. Find the matrix representation ![$[T]$](img1153.png) of
of  relative to the usual basis
relative to the usual basis
 . Find also
. Find also
![$[T]_{¥bf w}$](img1208.png) relative to the basis
relative to the basis
 .
.
また
 を求めよ.
を求めよ.