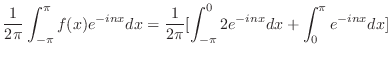Next: 演習問題 Up: フーリエ級数 Previous: 演習問題 目次 索引
 が
が![$[-L,L]$](img1746.png) で偶関数ならば,
で偶関数ならば,
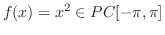 は偶関数,
は偶関数,
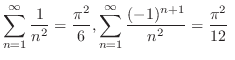 は奇関数となり,そのフーリエ係数は
は奇関数となり,そのフーリエ係数は
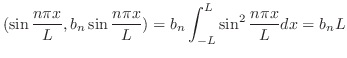 |
 |
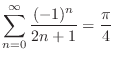 |
|
 |
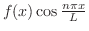 |
||
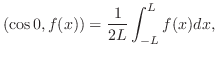 |
 |
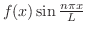 |
 が奇関数ならば,
が奇関数ならば,
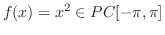 は奇関数,
は奇関数,
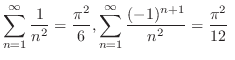 は偶関数となり,そのフーリエ係数は
は偶関数となり,そのフーリエ係数は
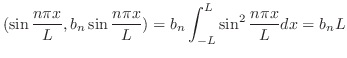 |
 |
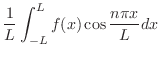 |
|
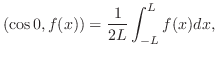 |
 |
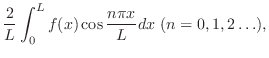 |
|
 |
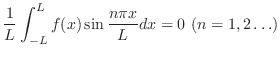 |
関数 が
が![$[0,L]$](img1818.png) で定義されているとき,
で定義されているとき,
![$\displaystyle f_{e}(-x) = \left\{\begin{array}{ll}
f(-x), & x \in [-L,0)\\
f(x), & x \in [0,L]
\end{array} \right. , \
f_{e}(x) \equiv f_{e}(x + 2L)$](img1819.png)
 の偶関数に拡張された関数
の偶関数に拡張された関数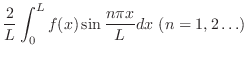 を偶関数拡張(even extension)といいます.また,
を偶関数拡張(even extension)といいます.また,
![$\displaystyle f_{o}(-x) = \left\{\begin{array}{ll}
-f(-x), & x \in [-L,0)\\
f(x), & x \in [0,L]
\end{array} \right. , f_{o}(x) \equiv f_{o}(x + 2L) $](img1821.png)
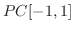 の奇関数に拡張された関数
の奇関数に拡張された関数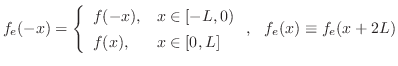 を奇関数拡張(odd extension)といいます.
を奇関数拡張(odd extension)といいます.
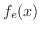 が
が![$[0,1]$](img1824.png) で定義されているとき,
で定義されているとき,
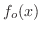 を求めよ.
を求めよ.解
![$\displaystyle f_{e}(x) = \left\{\begin{array}{rl}
-x+1,& x \in [-1,0)\\
x+1,& ...
...\begin{array}{rl}
x-1,& x \in [-1,0)\\
x+1,& x \in [0,1]
\end{array}\right . .$](img1826.png)
 の偶関数拡張
の偶関数拡張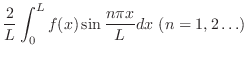 は区間
は区間![$[-L,L]$](img1746.png) で区分的に連続.したがって,
で区分的に連続.したがって,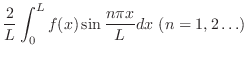 のフーリエ級数は次のように表わせます.
のフーリエ級数は次のように表わせます.
 |
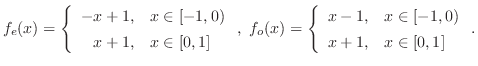 |
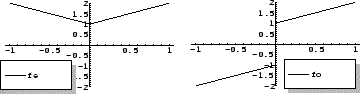 |
|
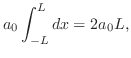 |
 |
 |
|
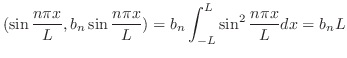 |
 |
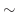 |
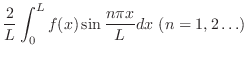 のフーリエ級数は
のフーリエ級数は![$[0,L]$](img1818.png) での
での のフーリエ級数,
のフーリエ級数,![$[-L,0]$](img1833.png) での
での の
偶関数拡張のフーリエ級数を表わします.これより
の
偶関数拡張のフーリエ級数を表わします.これより のフーリエ級数を
のフーリエ級数を のフーリエ余弦級数(Fourier cosine transform)といいます.
のフーリエ余弦級数(Fourier cosine transform)といいます.
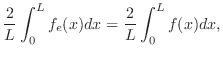
解
![$\displaystyle a_{0} = \frac{2}{\pi}\int_{0}^{\pi}f(x)dx = \frac{2}{\pi}\int_{0}...
...rac{x^2}{2}\mid_{0}^{\pi/2}] = \frac{2}{\pi}[\frac{\pi^2}{8}] = \frac{\pi}{4}, $](img1835.png)
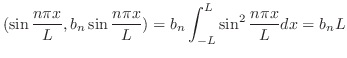 |
 |
 |
|
 |
![$\displaystyle \frac{2}{\pi}[\frac{x\sin{nx}}{n}\vert _{0}^{\pi/2} - \frac{1}{n}\int_{0}^{\pi/2}\sin{nx}dx ]$](img1837.png) |
||
 |
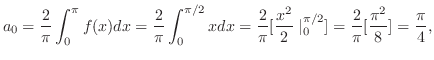 |
![$\displaystyle f(x) \sim \frac{\pi}{8} + \frac{1}{\pi}[(\pi - 2)\cos{x} - \cos{2...
...(\frac{\pi}{3} + \frac{2}{9})\cos{3x} + \cdots ] .
\ensuremath{ \blacksquare}
$](img1839.png)
偶関数拡張と同様に奇関数拡張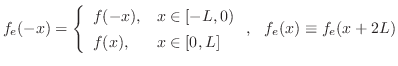 のフーリエ級数は関数列
のフーリエ級数は関数列
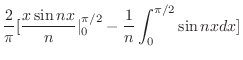 を用いて表わすことができます.つまり
を用いて表わすことができます.つまり
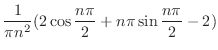 |
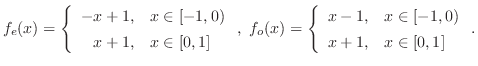 |
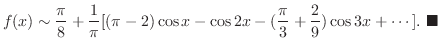 |
|
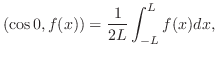 |
 |
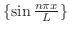 |
このようにして得たフーリエ級数を のフーリエ正弦級数(Fourier sine transform)といいます.
のフーリエ正弦級数(Fourier sine transform)といいます.
解
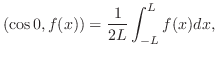 |
 |
![$\displaystyle \frac{2}{\pi}\int_{0}^{\pi/2}x\sin{nx}dx = \frac{2}{\pi}[-\frac{x\cos{nx}}{n}\mid_{0}^{\pi/2} + \frac{1}{n}\int_{0}^{\pi/2}\cos{nx}dx ]$](img1845.png) |
|
 |
![$\displaystyle \frac{2}{\pi}[-\frac{\frac{\pi}{2}\cos{\frac{n\pi}{2}}}{n} + \frac{1}{n^2}\sin{nx}\mid_{0}^{\pi/2}]$](img1846.png) |
||
 |
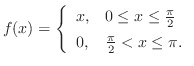 |
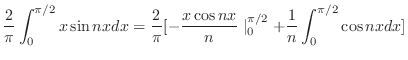
フーリエ級数の中に現われる
 と
と
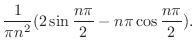 をEulerの公式
をEulerの公式
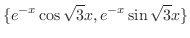 を用いて表わすと
を用いて表わすと
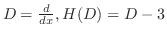 |
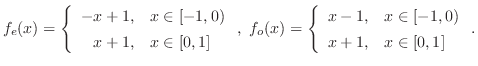 |
![$\displaystyle \frac{a_{0}}{2} + \sum_{n=1}^{\infty}[a_{n}(\frac{e^{in\pi x/L} + e^{-in\pi x/L}}{2}) + b_{n}(\frac{e^{in\pi x/L} - e^{-in\pi x/L}}{2i})]$](img1851.png) |
|
 |
![$\displaystyle \frac{a_{0}}{2} + \sum_{n=1}^{\infty}[(\frac{a_{n}-ib_{n}}{2})e^{in\pi x/L} + (\frac{a_{n} + ib_{n}}{2})e^{-in\pi x/L}]$](img1852.png) |
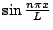 とおくと
とおくと のフーリエ級数は
のフーリエ級数は
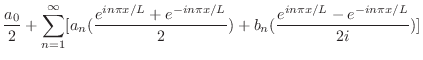
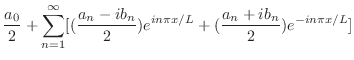
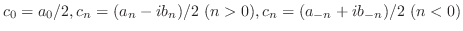
解
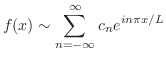 |
 |
![$\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx = \frac{1}{2\pi}[\int_{-\pi}^{0}2dx + \int_{0}^{\pi}dx] = \frac{3}{2},$](img1858.png) |
|
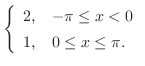 |
 |
![$\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)e^{-inx}dx = \frac{1}{2\pi}[\int_{-\pi}^{0}2e^{-inx}dx + \int_{0}^{\pi}e^{-inx}dx]$](img1860.png) |
|
 |
![$\displaystyle -\frac{1}{i\pi n}e^{-inx}\mid_{-\pi}^{0} - \frac{1}{i2n\pi n}e^{-inx}\mid_{0}^{\pi} = \frac{i}{n\pi}[1-e^{in\pi}] + \frac{1}{2n\pi}[e^{-in\pi}-1]$](img1861.png) |
||
 |
![$\displaystyle \frac{i}{n\pi}[1-(-1)^{n}] + \frac{i}{2n\pi}[(-1)^{n} - 1] = \lef...
...
0, & n \mbox{even}\\
\frac{i}{n\pi}, & n \mbox{odd} .
\end{array}\right .$](img1862.png) |