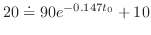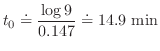Next: 演習問題 Up: 1階微分方程式 Previous: 演習問題 目次 索引
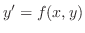
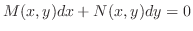
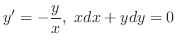
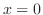 の場合を除けば同じものとして扱えます.一般に上の2つの形の微分方程式は,形式的に同じものとして扱うことができます.
の場合を除けば同じものとして扱えます.一般に上の2つの形の微分方程式は,形式的に同じものとして扱うことができます.
たぶん1階の微分方程式の中でもっとも簡単なのは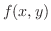 が
が だけの関数のときでしょう.この場合,微分方程式は
だけの関数のときでしょう.この場合,微分方程式は
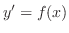
 について積分すると一般解
について積分すると一般解
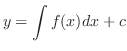
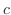 は任意の定数です.
は任意の定数です.
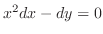 の一般解を求めよ.
の一般解を求めよ.
解
与えられた微分方程式は
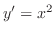 と書き直せる.よって両辺を
と書き直せる.よって両辺を について積分して一般解
について積分して一般解
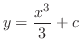

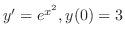 を解け.
を解け.
解
この場合,微分方程式
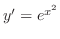 を
を について積分したのでは初期値問題は解けない.なぜならば
について積分したのでは初期値問題は解けない.なぜならば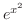 の原始関数は初等関数ではない.そこで不定積分の代わりに定積分を用いる.
の原始関数は初等関数ではない.そこで不定積分の代わりに定積分を用いる.
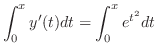
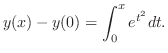
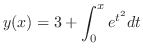

こういう解の表わし方に慣れてないかも知れませんが,これは立派な解です.なぜならばどんな特定な値 に対しても
に対しても
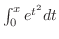 は数値的に何桁までも正確に近似できるからです.
は数値的に何桁までも正確に近似できるからです.
次に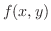 が
が の関数と
の関数と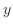 の関数の積で表わされる場合を考えます.
の関数の積で表わされる場合を考えます.
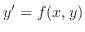 が
が
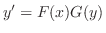
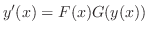
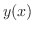 を求めます.左辺に
を求めます.左辺に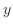 の関数,右辺に
の関数,右辺に の関数となるように書き直すと
の関数となるように書き直すと
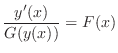
 について積分すると
について積分すると
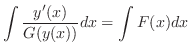
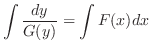
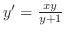 を解け.
を解け.解 この微分方程式は形式的に
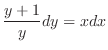
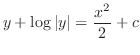
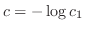 を用いて書き直すと,
を用いて書き直すと,
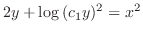

上の例題で
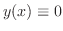 は元の式の解ですが,求めた一般解の中には
は元の式の解ですが,求めた一般解の中には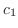 をどのような値にとっても
をどのような値にとっても
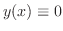 は含まれていません.このように微分方程式の解なのに,一般解の任意定数にどのような値を与えても得られない解を,その微分方程式の特異解(singular solution)といいます.他にも消えてしまった解があるかもしれませんが,これは変数分離形ではよくおきることです.そこで私たちは1.7節までの間,形式的に求めたものを解として扱います.
は含まれていません.このように微分方程式の解なのに,一般解の任意定数にどのような値を与えても得られない解を,その微分方程式の特異解(singular solution)といいます.他にも消えてしまった解があるかもしれませんが,これは変数分離形ではよくおきることです.そこで私たちは1.7節までの間,形式的に求めたものを解として扱います.
次の例題はNewtonの冷却の法則(Newton's law of cooling)を用います.実験より温度が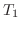 と
と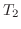 の2物体が向かい合っているとき,高温の物体から低温の物体へ
の2物体が向かい合っているとき,高温の物体から低温の物体へ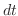 時間に移る熱量
時間に移る熱量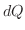 は,
は,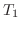 と
と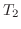 の温度差が小さいとき近似的に比例して次の式で与えらることがわかっています.
の温度差が小さいとき近似的に比例して次の式で与えらることがわかっています.
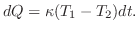
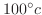 に熱せられた鉄球を
に熱せられた鉄球を
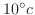 に保たれた水の中に入れる.
に保たれた水の中に入れる.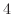 分後鉄球の温度は
分後鉄球の温度は
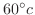 でした.鉄球の温度が
でした.鉄球の温度が
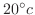 になるのは何分後か求めよ.
になるのは何分後か求めよ.解 Newtonの冷却の法則を使ってこの問題を定式化すると
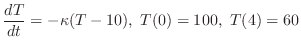
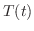 は時間
は時間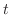 分後の鉄球の温度を表わしている.変数を分離し積分すると
分後の鉄球の温度を表わしている.変数を分離し積分すると
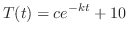
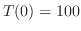 と
と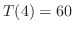 より
より
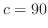 と
と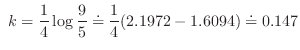
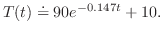
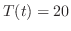 となる
となる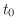 を求めると,
を求めると,