Next: 演習問題 Up: 1階微分方程式 Previous: 演習問題 目次 索引
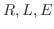
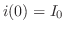 をかけると
をかけると
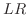
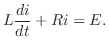
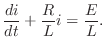 ,
,
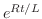 より
より
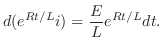
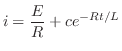 について線形なので前節で学んだ方法で解くことができます.
について線形なので前節で学んだ方法で解くことができます.
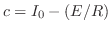 を解け.
を解け.
解
この方程式はBernoulliの方程式である.そこで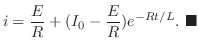 を両辺にかけて整理すると
を両辺にかけて整理すると
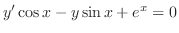
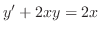 とおくと
とおくと
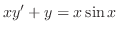 より
より
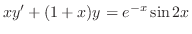
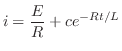 について線形なので標準形に直し,積分因子
について線形なので標準形に直し,積分因子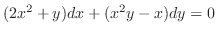 を求めると
を求めると
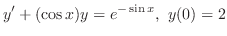 となる.これを標準形にかけると
となる.これを標準形にかけると
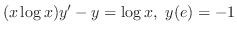
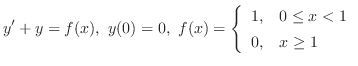

Bernoulliの方程式を解くときにあらわれた
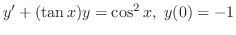 の形からもっと一般的な場合を考えることができます.
の形からもっと一般的な場合を考えることができます.
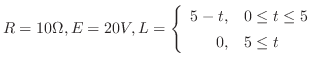
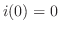 とおくと,
とおくと,
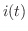 より
より
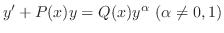
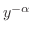 を解け.
を解け.
解
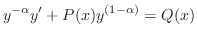 とおくと
とおくと
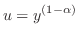 .
よって与えられた微分方程式は
.
よって与えられた微分方程式は
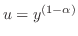
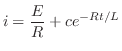 について線形なので積分因子
について線形なので積分因子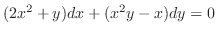 を求めると
を求めると
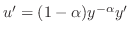
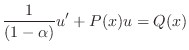
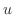
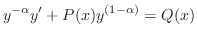 を代入すると
を代入すると
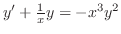

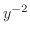
 がわかった場合
がわかった場合
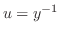
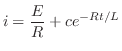 に関する線形微分方程式を得ます.
に関する線形微分方程式を得ます.
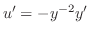 の解
の解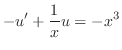 が与えられているとき,方程式を解け.
が与えられているとき,方程式を解け.
解
この微分方程式はRiccatiの方程式である.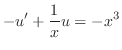 はこの方程式のひとつの解であるから
はこの方程式のひとつの解であるから
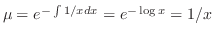
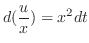 .これらを微分方程式に代入すると,
.これらを微分方程式に代入すると,
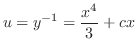
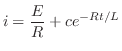 に関する線形微分方程式
に関する線形微分方程式
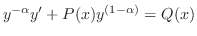
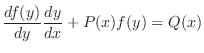 を得,これを両辺にかけると
を得,これを両辺にかけると
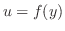
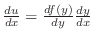
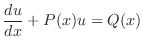 より
より