Next: 演習問題 Up: 連立線形微分方程式 Previous: 連立線形微分方程式 目次 索引
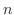 個の未知関数をもつ微分方程式の系.つまり連立線形微分方程式(system of linear differential equation)
個の未知関数をもつ微分方程式の系.つまり連立線形微分方程式(system of linear differential equation)
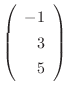
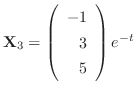
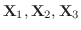
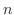 個の微分可能な関数
個の微分可能な関数
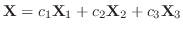 をこの方程式の解(solution)といいます.また,
をこの方程式の解(solution)といいます.また,
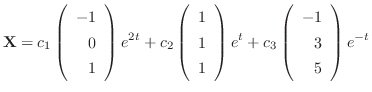 のとき,この微分方程式を同次方程式(homogeneous equation)といいます.
のとき,この微分方程式を同次方程式(homogeneous equation)といいます.
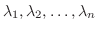 は明らかに,同次方程式
は明らかに,同次方程式
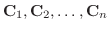 の解です.そこでそれ以外の解を捜すため,1階の線形微分方程式
の解です.そこでそれ以外の解を捜すため,1階の線形微分方程式
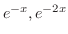 の解が
の解が
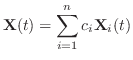 で与えられたことを思い出します.このことから多分
で与えられたことを思い出します.このことから多分
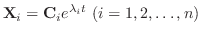 は
は
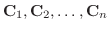 の解になるのではと見当をつけます.ただし
の解になるのではと見当をつけます.ただし
 は任意の定数ベクトルとします.これを
は任意の定数ベクトルとします.これを
 に代入すると,
に代入すると,
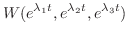
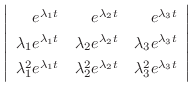 はどんな
はどんな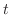 に対しても0にならないことに注意すると,
に対しても0にならないことに注意すると,
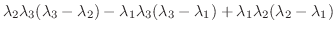
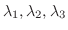
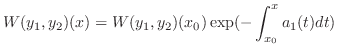 は
は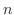 次の単位行列を表わします.
次の単位行列を表わします.
このことから,
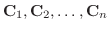 の自明でない解を見つけるには
の自明でない解を見つけるには
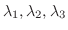
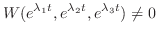 でないベクトル
でないベクトル
 を見つければよいことがわかります.この連立方程式を満たす
を見つければよいことがわかります.この連立方程式を満たす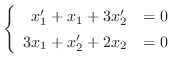 を行列
を行列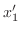 の固有値(eigenvalue).そして0でないベクトル
の固有値(eigenvalue).そして0でないベクトル
 を
を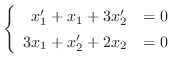 に対する固有ベクトル(eigenvector)といいます.ところで連立方程式
に対する固有ベクトル(eigenvector)といいます.ところで連立方程式
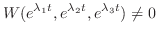 でない解をもつための必要十分条件は
でない解をもつための必要十分条件は
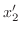 であることを線形代数学で学びました.また
であることを線形代数学で学びました.また
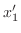 は
は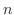 次の多項式になり
次の多項式になり
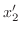 を行列
を行列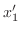 の特性方程式(characteristic equation)ということも学びました.そこで私たちは,特性方程式を解いて固有値
の特性方程式(characteristic equation)ということも学びました.そこで私たちは,特性方程式を解いて固有値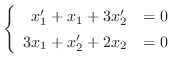 を求め,連立方程式
を求め,連立方程式
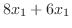 を解いて,固有ベクトルを求めることができます.つまり非常に難しい微分方程式の問題が簡単な線形代数の問題に還元されました.
を解いて,固有ベクトルを求めることができます.つまり非常に難しい微分方程式の問題が簡単な線形代数の問題に還元されました.
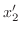 を解け.
を解け.解
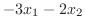
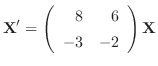 である.次に固有値
である.次に固有値
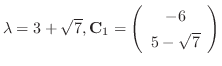 に対する固有ベクトル
に対する固有ベクトル
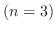 は
は
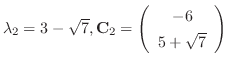
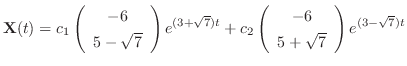 |
 |
 |
|
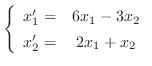 |
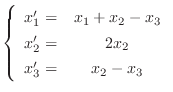 |
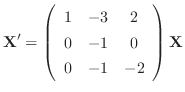 は任意の定数,
は任意の定数,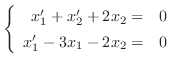 ,
,
 となる.したがって,固有ベクトルCは
となる.したがって,固有ベクトルCは
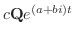 で表わされ,
で表わされ,
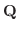 はこの微分方程式のひとつの解である.
はこの微分方程式のひとつの解である.
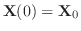 に対する固有ベクトルは
に対する固有ベクトルは
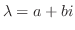 |
 |
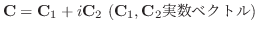 |
|
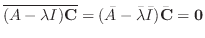 |
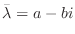 |
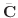 で表わされ,
で表わされ,
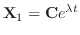 もこの微分方程式のひとつの解である.同様に固有値
もこの微分方程式のひとつの解である.同様に固有値
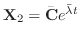 に対する固有ベクトルは
に対する固有ベクトルは
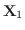 |
 |
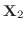 |
|
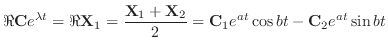 |
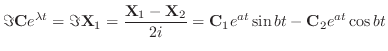 |
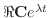 で表わされ,
で表わされ,
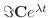 もこの微分方程式のひとつの解である.ここで
もこの微分方程式のひとつの解である.ここで
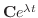 は一次独立なので
は一次独立なので
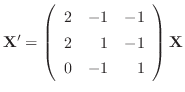 は一般解になると思われる.次の定理で述べるが,確かにこれは一般解である.よって一般解は
は一般解になると思われる.次の定理で述べるが,確かにこれは一般解である.よって一般解は
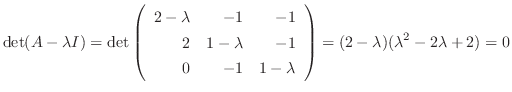

行列 の係数が定数で,
の係数が定数で, 個の異なる固有値をもつとき,次の定理が成り立ちます.
個の異なる固有値をもつとき,次の定理が成り立ちます.
|
定理 3..1 同次連立微分方程式
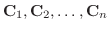 の の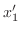 が が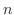 次の定数行列で 次の定数行列で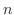 個の異なる固有値 個の異なる固有値
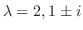 とそれに対する固有ベクトル とそれに対する固有ベクトル
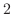 をもつならば,この微分方程式の一般解は をもつならば,この微分方程式の一般解は
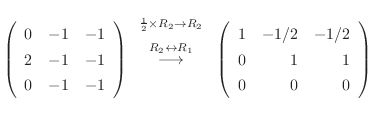
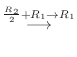 はそれぞれ はそれぞれ
 の解であり,また一次独立である. の解であり,また一次独立である. |
証明
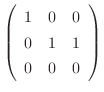 の場合
の場合
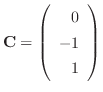 |
 |
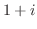 |
|
 |
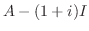 |
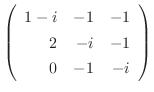 は異なる固有値なので
は異なる固有値なので
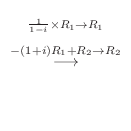

ここにでてきた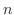 個の一次独立な解を微分方程式
個の一次独立な解を微分方程式
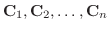 の基本解(fundamental solution)といいます.
連立同次線形微分方程式はいつも
の基本解(fundamental solution)といいます.
連立同次線形微分方程式はいつも
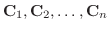 の形で与えられるわけではありません.こんなときはまず
の形で与えられるわけではありません.こんなときはまず
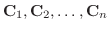 の形に変換する必要があります.
の形に変換する必要があります.
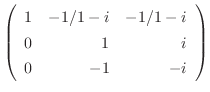 .
.
解
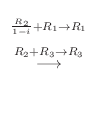 と
と
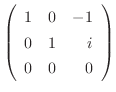 について解くと,
について解くと,
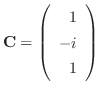 |
 |
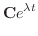 |
|
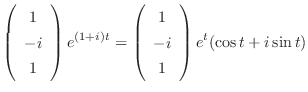 |
 |
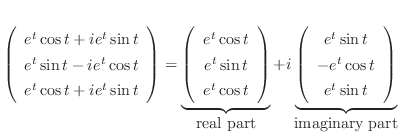 |
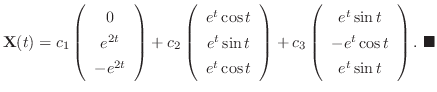
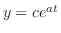 ,
,
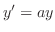 となる.よって定理3.1より一般解は
となる.よって定理3.1より一般解は