Next: 2.5 解答 Up: 演習問題解答 Previous: 2.3 解答 索引
2.4
1.
(a) 補助方程式
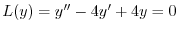 の特性方程式は
の特性方程式は
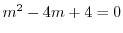 より特性根
より特性根
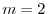 重根を得る.よって余関数
重根を得る.よって余関数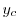 は
は
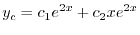
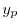 を未定係数法を用いて求める.
を未定係数法を用いて求める.
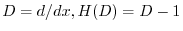 とおくと,
とおくと,
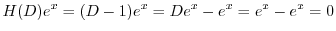
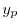 は
は
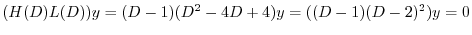
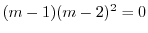 より基本解は
より基本解は
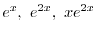 であるが,
であるが,
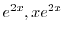 は余関数の解なので省くと
は余関数の解なので省くと
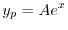
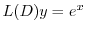 に代入すると
に代入すると
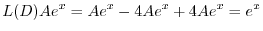
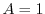 を得る.これより特殊解は
を得る.これより特殊解は
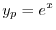
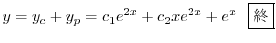
(b) 補助方程式
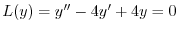 の特性方程式は
の特性方程式は
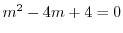 より特性根
より特性根
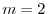 重根を得る.よって余関数
重根を得る.よって余関数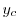 は
は
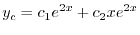
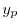 を未定係数法を用いて求める.
を未定係数法を用いて求める.
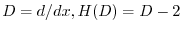 とおくと,
とおくと,
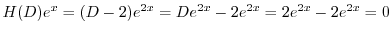
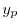 は
は
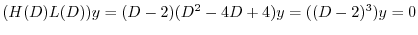
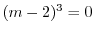 より基本解は
より基本解は
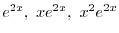 であるが,
であるが,
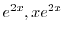 は余関数の解なので省くと
は余関数の解なので省くと
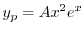
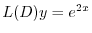 に代入すると
に代入すると
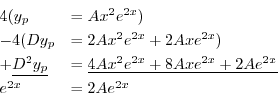
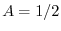 を得る.これより特殊解は
を得る.これより特殊解は
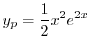
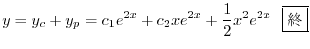
(c) 補助方程式
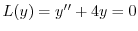 の特性方程式は
の特性方程式は
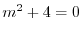 より特性根
より特性根
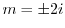 を得る.よって余関数
を得る.よって余関数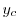 は
は
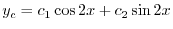
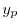 を未定係数法を用いて求める.
を未定係数法を用いて求める.
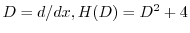 とおくと,
とおくと,
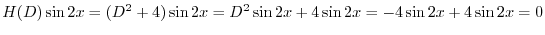
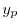 は
は
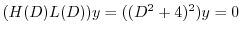
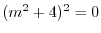 より基本解は
より基本解は
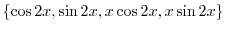
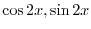 は余関数の解なので省くと
は余関数の解なので省くと
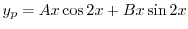
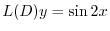 に代入すると
に代入すると
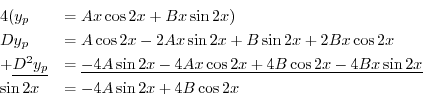
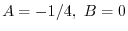 を得る.これより特殊解は
を得る.これより特殊解は
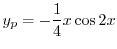
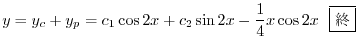
(d) 補助方程式
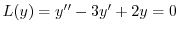 の特性方程式は
の特性方程式は
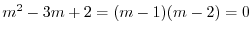 より特性根
より特性根
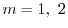 を得る.よって余関数
を得る.よって余関数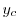 は
は
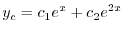
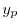 を未定係数法を用いて求める.重ね合わせの原理より
を未定係数法を用いて求める.重ね合わせの原理より
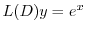 の特殊解
の特殊解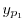 ,
,
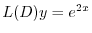 の特殊解
の特殊解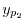 ,
,
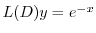 の特殊解
の特殊解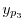 を求めれば
を求めれば
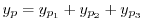 で与えられる.
で与えられる.
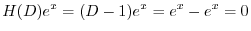
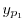 は
は
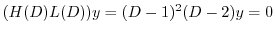
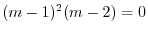 より基本解は
より基本解は
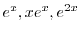 であるが,
であるが,
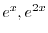 は余関数の解なので省くと
は余関数の解なので省くと
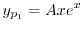
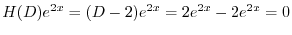
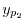 は
は
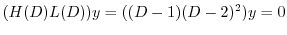
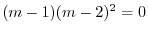 より基本解は
より基本解は
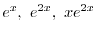 であるが,
であるが,
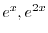 は余関数の解なので省くと
は余関数の解なので省くと
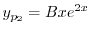
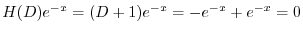
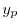 は
は
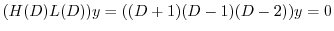
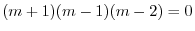 より基本解は
より基本解は
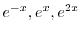 であるが,
であるが,
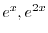 は余関数の解なので省くと
は余関数の解なので省くと
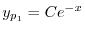
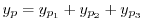 を
を
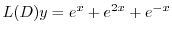 に代入すると
に代入すると
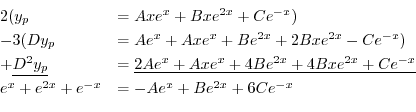
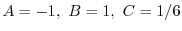 を得る.これより特殊解は
を得る.これより特殊解は
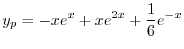
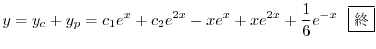
(e) 補助方程式
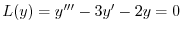 の特性方程式は
の特性方程式は
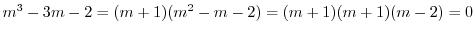 より特性根
より特性根
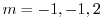 を得る.よって余関数
を得る.よって余関数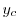 は
は
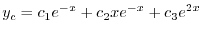
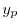 を未定係数法を用いて求める.
を未定係数法を用いて求める.
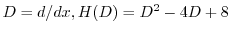 とおくと,
とおくと,
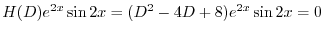
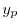 は
は
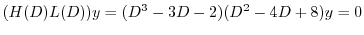
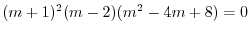 より基本解は
より基本解は
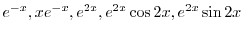
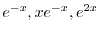 は余関数の解なので省くと
は余関数の解なので省くと
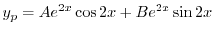
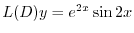 に代入すると
に代入すると
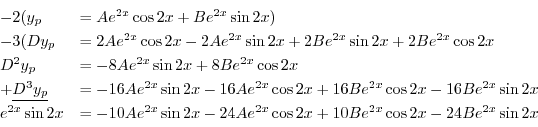
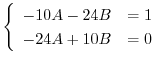
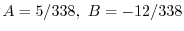 を得る.これより特殊解は
を得る.これより特殊解は
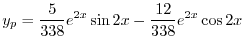
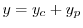 |
 |
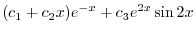 |
|
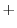 |
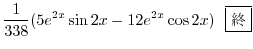 |
(f) 補助方程式
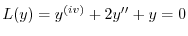 の特性方程式は
の特性方程式は
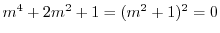 より特性根
より特性根
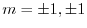 を得る.よって余関数
を得る.よって余関数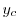 は
は
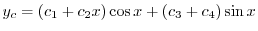
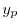 を未定係数法を用いて求める.
を未定係数法を用いて求める.
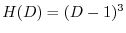 とおくと,
とおくと,
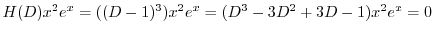
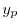 は
は
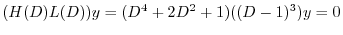
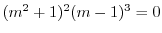 より基本解は
より基本解は
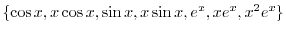
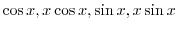 は余関数の解なので省くと
は余関数の解なので省くと
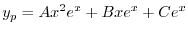
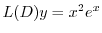 に代入すると
に代入すると
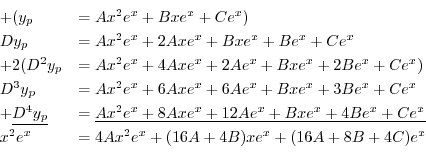
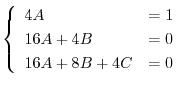
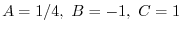 を得る.これより特殊解は
を得る.これより特殊解は
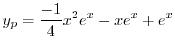
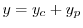 |
 |
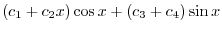 |
|
 |
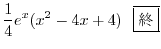 |