Next: 6.9 解答 Up: 演習問題詳解 Previous: 6.7 解答 索引
6.8
1.
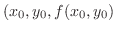
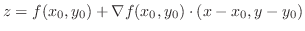
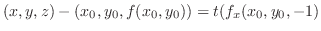 |
 |
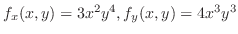 |
|
 |
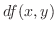 |
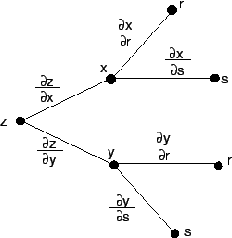
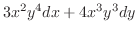 とおき,
とおき,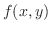 の全微分を求めると,
の全微分を求めると,
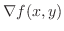
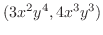
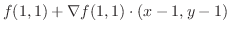 を求める.ここでは,
を求める.ここでは,
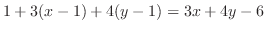
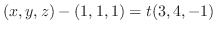
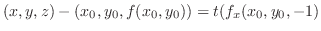 |
 |
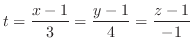 |
|
 |
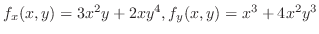 |
||
 |
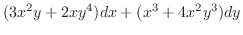 |
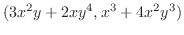 とおき,
とおき,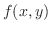 の全微分を求めると,
の全微分を求めると,
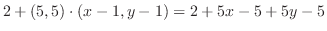
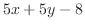
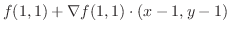 を求める.ここでは,
を求める.ここでは,
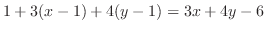
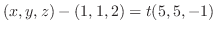
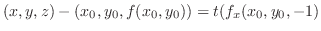 |
 |
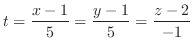 |
|
 |
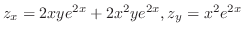 |
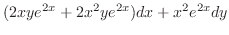 とおき,
とおき,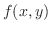 の全微分
の全微分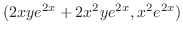 を求める.
を求める.
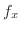 |
 |
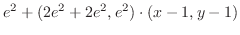 |
|
 |
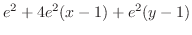 |
||
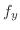 |
 |
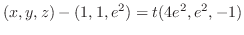 |
|
 |
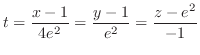 |
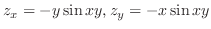
次に,
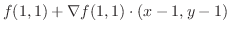 を求める.ここでは,直接求める.
を求める.ここでは,直接求める.
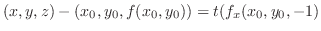 |
 |
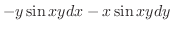 |
|
 |
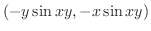 |
||
 |
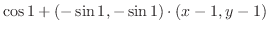 |
||
 |
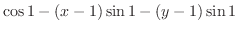 |
2.
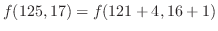
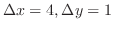 の項を消去すると
の項を消去すると
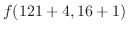
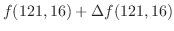
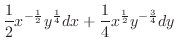 の項を消去すると
の項を消去すると
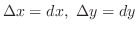
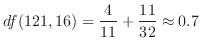
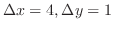 の項を消去すると
の項を消去すると
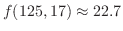
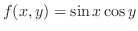
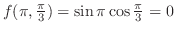
3.
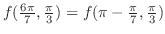
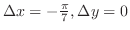
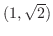 を通る接線の方程式は
を通る接線の方程式は
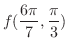
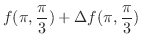 .よって点
.よって点
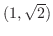 を通る法線の方程式は
を通る法線の方程式は
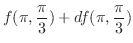
4.
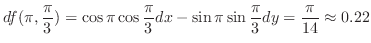
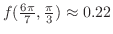
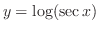 は曲面
は曲面
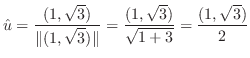 に直交するので,接平面
に直交するので,接平面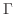 上に任意の点
上に任意の点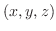 を取ると,ベクトル
を取ると,ベクトル
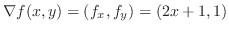 と
と
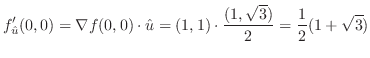 は直交する.よって,接平面の方程式は
は直交する.よって,接平面の方程式は
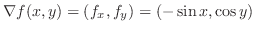
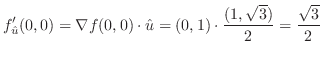
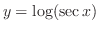 と同方向にあるので,法線上に任意の点
と同方向にあるので,法線上に任意の点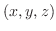 を取ると,
を取ると,
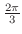
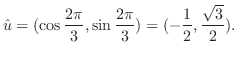
5.
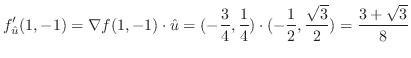
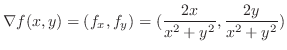 . これを
. これを
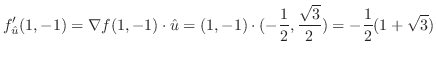 に代入すると
に代入すると
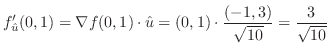 . よって,
. よって,
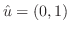 .次に
.次に
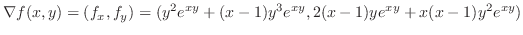
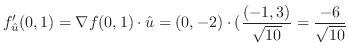 を計算すると
を計算すると
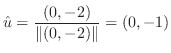

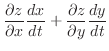 のときの
のときの
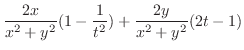 は極小値,
は極小値,
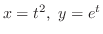 のときの
のときの
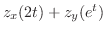 は極大値.
は極大値.
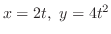
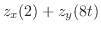 .これを
.これを
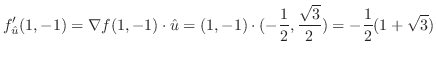 に代入すると
に代入すると
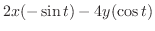 . よって,
. よって,
 .次に
.次に
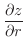
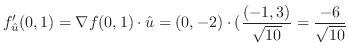 を計算すると
を計算すると
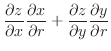
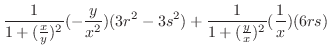
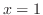 のときの
のときの
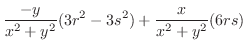 は極小値,
は極小値, 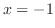 のときの
のときの
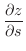 は極大値.
は極大値.
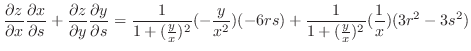
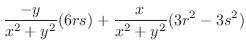 .これを
.これを
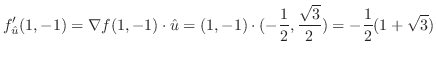 に代入すると
に代入すると
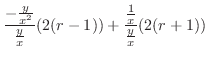 . よって,
. よって,
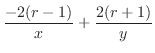 .次に
.次に
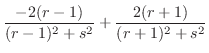
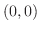 で
で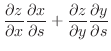 となるので,
となるので,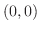 では極値はとらない.
では極値はとらない.
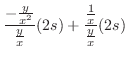 で
で
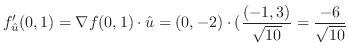 を計算すると
を計算すると
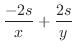
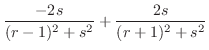 のときの
のときの
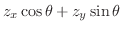 は極小値
は極小値