Next: 6.8 解答 Up: 演習問題詳解 Previous: 6.6 解答 索引
6.7
1.
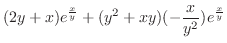
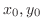 について解くと
について解くと
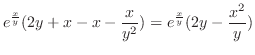 .
次に
.
次に
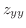 ,
,
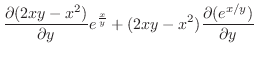 より
より
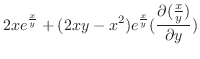 となるので
となるので
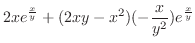 は極小値.
は極小値.
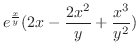 より
より
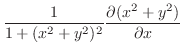 .
.
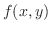 が
が
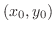 で極値をとるならば
で極値をとるならば
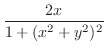
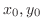 について解く.
について解く.
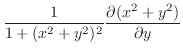 より
より
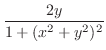 .よって
.よって
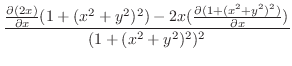 .また,
.また,
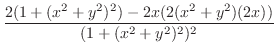 より
より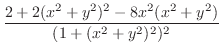 .
.
次に
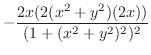 .
.
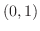 では
では
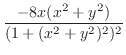
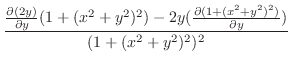 より
より
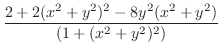 .
.
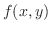 が
が
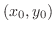 で極値をとるならば
で極値をとるならば
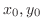 について解く.式(10.1)より
について解く.式(10.1)より
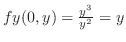 を式(10.2)に代入すると,
を式(10.2)に代入すると,
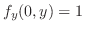
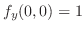 .したがって,
.したがって,
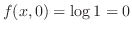 .
次に
.
次に
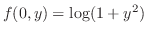 .
.
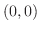 では
では
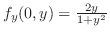
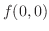 は極値でない.
は極値でない.
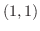 では
では
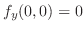
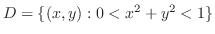 は極小値.
は極小値.
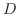 より
より
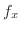 |
 |
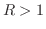 |
|
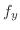 |
 |
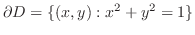 |
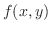 が
が
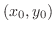 で極値をとるならば
で極値をとるならば
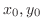 について解く.式(10.4)より
について解く.式(10.4)より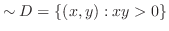 となり,これを式(10.3)に代入すると,
となり,これを式(10.3)に代入すると,
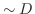
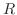 .したがって,
.したがって,
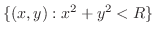 .
次に
.
次に
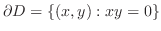 |
 |
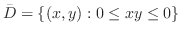 |
|
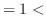 |
 |
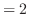 |
|
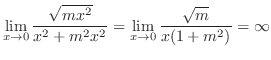 |
 |
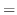 |
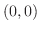 では
では
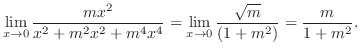
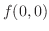 は極値でない.
は極値でない.
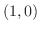 では
では
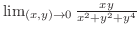
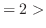 は極小値.
は極小値.
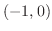 では
では
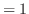
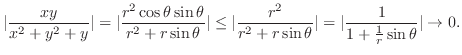 は極小値.
は極小値.
2.
2変数関数のTaylorの定理
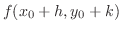 |
 |
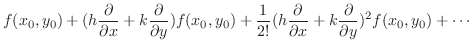 |
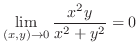
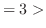
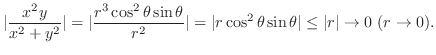
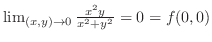
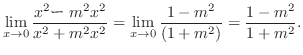
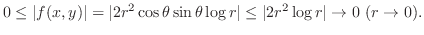
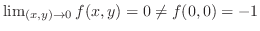
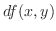
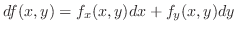
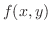 |
 |
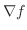 |