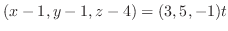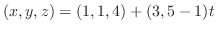Next: 6.5 全微分 Up: 確認問題詳解 Previous: 6.3 関数の極限 索引
1.
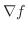 |
 |
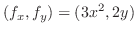 |
|
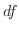 |
 |
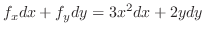 |
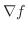 |
 |
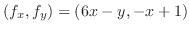 |
|
 |
 |
 |
 |
 |
 |
|
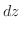 |
 |
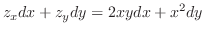 |
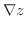 |
 |
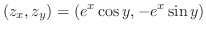 |
|
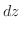 |
 |
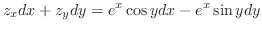 |
2.
(a) 求める平面上に任意の点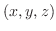 と,点
と,点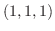 より作られるベクトルは
より作られるベクトルは
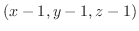 で与えられる.このベクトルと法線ベクトル
で与えられる.このベクトルと法線ベクトル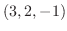 は直交するので,その内積は零である.これより,
は直交するので,その内積は零である.これより,
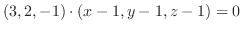
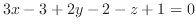
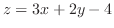
法線の方程式は,法線上に任意の点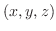 をとると,
をとると,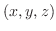 と
と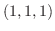 が作るベクトルは,法線ベクトルのスカラー倍となることが分かる.したがって,
が作るベクトルは,法線ベクトルのスカラー倍となることが分かる.したがって,
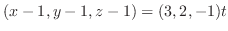
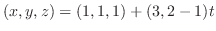
(b) 接平面を求めるには,平面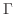 上の1点と法線ベクトルがあればよい.そこで,まず法線ベクトル
上の1点と法線ベクトルがあればよい.そこで,まず法線ベクトル
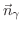 を求める.曲面が
を求める.曲面が
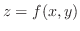 で与えられるとき,法線ベクトルは
で与えられるとき,法線ベクトルは
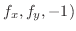 で求められる.したがって,
で求められる.したがって,
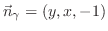
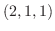 は平面
は平面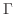 上の点なので,この点を通る法線ベクトルを求めると
上の点なので,この点を通る法線ベクトルを求めると
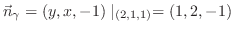
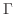 上に任意の点
上に任意の点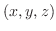 と点
と点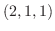 が作るベクトル
が作るベクトル
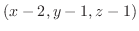 と法線ベクトルは直交するので,
と法線ベクトルは直交するので,
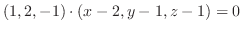
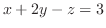
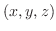 をとると,
をとると,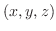 と
と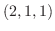 が作るベクトルは,法線ベクトルのスカラー倍となることが分かる.したがって,
が作るベクトルは,法線ベクトルのスカラー倍となることが分かる.したがって,
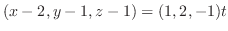
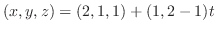
(c) 接平面を求めるには,平面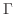 上の1点と法線ベクトルがあればよい.そこで,まず法線ベクトル
上の1点と法線ベクトルがあればよい.そこで,まず法線ベクトル
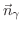 を求める.曲面が
を求める.曲面が
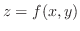 で与えられるとき,法線ベクトルは
で与えられるとき,法線ベクトルは
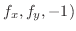 で求められる.したがって,
で求められる.したがって,
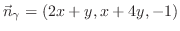
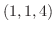 は平面
は平面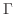 上の点なので,この点を通る法線ベクトルを求めると
上の点なので,この点を通る法線ベクトルを求めると
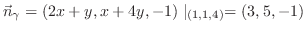
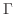 上に任意の点
上に任意の点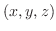 と点
と点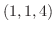 が作るベクトル
が作るベクトル
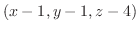 と法線ベクトルは直交するので,
と法線ベクトルは直交するので,
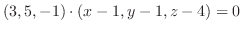
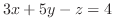
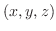 をとると,
をとると,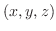 と
と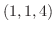 が作るベクトルは,法線ベクトルのスカラー倍となることが分かる.したがって,
が作るベクトルは,法線ベクトルのスカラー倍となることが分かる.したがって,