Next: ベクトル3重積(Vector triple product) Up: 内積・外積の応用(Applicatin of Inner product Previous: 面積ベクトル(Area vector) 目次 索引
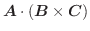 をスカラー3重積といい,
をスカラー3重積といい,
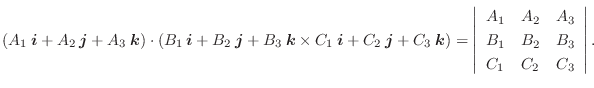
ベクトル
 が同一平面上に乗るとき
が同一平面上に乗るとき
 は共面であるまたは1次従属であるといいます.また,
は共面であるまたは1次従属であるといいます.また,
 が同一平面上にならないならば,共面でないまたは1次独立であるといいます.
が同一平面上にならないならば,共面でないまたは1次独立であるといいます.
スカラー3重積の絶対値は,
 で作る平行六面体の体積と考えることができます.そこで,
ベクトル
で作る平行六面体の体積と考えることができます.そこで,
ベクトル
 が共面か共面でないかを調べるとき, スカラー三重積を使うと簡単に調べられます.つまり
が共面か共面でないかを調べるとき, スカラー三重積を使うと簡単に調べられます.つまり
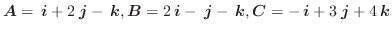 は共面でないことを示せ.
は共面でないことを示せ.
解
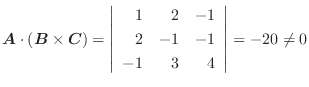 .よって共面でない.
.よって共面でない.
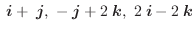 は共面か共面でないか調べよ.
は共面か共面でないか調べよ.
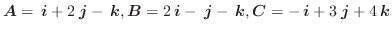 は共面ないことを示せ.
は共面ないことを示せ.
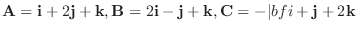 とするとき,
とするとき,
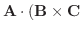 を求めよ.
を求めよ.
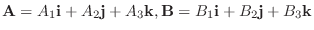 とする.
とする.
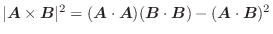 を示せ..
を示せ..