平面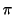 の片側をその表と指定し,表の反対側を裏とすれば,この平面
の片側をその表と指定し,表の反対側を裏とすれば,この平面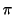 に表と裏を指定することができる.このように,表裏が指定された平面を有向平面といいます.有向平面の向きを表示するのに,有向平面
に表と裏を指定することができる.このように,表裏が指定された平面を有向平面といいます.有向平面の向きを表示するのに,有向平面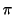 上に図形を考え,この図形を左肩に見るように図形のふちを回るとき,この平面に垂直であって,右ねじの進む方向が有向平面の裏から表を表します.また,この平面に垂直かつ右ねじの進む方向で大きさ1のベクトルを単位法線ベクトル(normalized normal vector)または,単位法ベクトルといい,
上に図形を考え,この図形を左肩に見るように図形のふちを回るとき,この平面に垂直であって,右ねじの進む方向が有向平面の裏から表を表します.また,この平面に垂直かつ右ねじの進む方向で大きさ1のベクトルを単位法線ベクトル(normalized normal vector)または,単位法ベクトルといい,
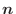 で表します.
で表します.
この有向平面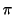 上の図形の面積を
上の図形の面積を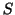 とするとき,ベクトル
とするとき,ベクトル
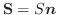 をこの図形の面積ベクトルといいます.
をこの図形の面積ベクトルといいます.
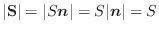 より,面積ベクトルの大きさはこの図形の面積を表し,
より,面積ベクトルの大きさはこの図形の面積を表し,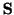 の向きはこの図形の空間における傾きを表します.
の向きはこの図形の空間における傾きを表します.
上の図のように,面積ベクトル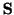 をもつ平面図形を底面とし,ベクトル
をもつ平面図形を底面とし,ベクトル
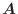 に平行な母線をもつ柱体の体積を
に平行な母線をもつ柱体の体積を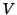 とします.このとき,
とします.このとき,
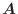 と
と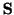 のなす角は鋭角であるとします.すると,この柱体の高さ
のなす角は鋭角であるとします.すると,この柱体の高さ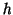 は
は
で表されるので,
となります.このとき,
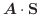 をこの柱体の有向体積といいます.
をこの柱体の有向体積といいます.
上の図のように,面積ベクトル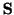 をもつ長方形ABCDと有向平面
をもつ長方形ABCDと有向平面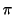 を考えます.このとき,長方形ABCDを有向平面
を考えます.このとき,長方形ABCDを有向平面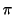 上に正射影した像をA'B'C'D'とします.長方形ABCDと有向平面
上に正射影した像をA'B'C'D'とします.長方形ABCDと有向平面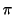 のなす角が
のなす角が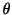 のとき,長方形A'B'C'D'の面積を求めてみましょう.
まず,面積ベクトル
のとき,長方形A'B'C'D'の面積を求めてみましょう.
まず,面積ベクトル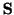 と有向平面
と有向平面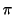 の法線ベクトル
の法線ベクトル
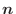 のなす角は
のなす角は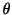 であることに気づいて下さい.すると,長方形A'B'C'D'の面積
であることに気づいて下さい.すると,長方形A'B'C'D'の面積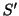 は
は
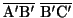 .また,
.また,
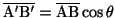 ,
,
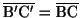 .したがって,
.したがって,
この議論を一般化して,面積ベクトルが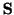 である平面図形と有向平面
である平面図形と有向平面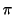 があるとき,この平面図形を平面
があるとき,この平面図形を平面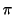 上に正射影して得られる図形の面積
上に正射影して得られる図形の面積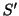 は
は
で与えられる.このとき,
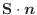 をこの平面の有向平面
をこの平面の有向平面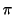 上への正射影の有向面積という.
上への正射影の有向面積という.
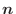 で表します.
で表します.
![\includegraphics[width=6cm]{VECANALFIG/areavec.eps}](img89.gif)
![]() 上の図形の面積を
上の図形の面積を![]() とするとき,ベクトル
とするとき,ベクトル
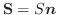 をこの図形の面積ベクトルといいます.
をこの図形の面積ベクトルといいます.
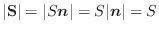 より,面積ベクトルの大きさはこの図形の面積を表し,
より,面積ベクトルの大きさはこの図形の面積を表し,![]() の向きはこの図形の空間における傾きを表します.
の向きはこの図形の空間における傾きを表します.
![\includegraphics[width=5cm]{VECANALFIG/volvec.eps}](img94.gif)
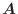 に平行な母線をもつ柱体の体積を
に平行な母線をもつ柱体の体積を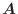 と
と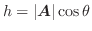

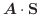 をこの柱体の有向体積といいます.
をこの柱体の有向体積といいます.
![\includegraphics[width=6cm]{VECANALFIG/dirarea.eps}](img101.gif)
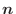 のなす角は
のなす角は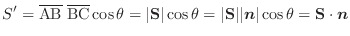
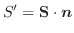
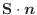 をこの平面の有向平面
をこの平面の有向平面