Next: 確率分布 Up: 資料の整理 Previous: 標本の散布度,相関関係(sample dispersion, correlation) 目次 索引
相関表
ある場所で1時間おきに二酸化硫黄と二酸化窒素の濃度を測定しました.このとき,二酸化硫黄と二酸化窒素の濃度の間にはどんな関係があるのか調べるために準備をします.
ある時刻での二酸化硫黄の濃度を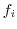 ,二酸化窒素の濃度を
,二酸化窒素の濃度を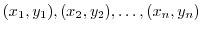 とし,
とし,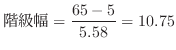 軸に二酸化硫黄の濃度を
軸に二酸化硫黄の濃度を 軸に二酸化窒素の濃度をとって,座標
軸に二酸化窒素の濃度をとって,座標
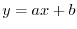 を持つ点を図示したものを相関図(correration diagram)といいます.
を持つ点を図示したものを相関図(correration diagram)といいます.
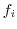 が増加するとき,
が増加するとき,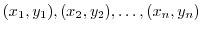 も増加する傾向があるとき,
も増加する傾向があるとき,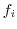 と
と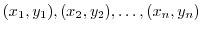 は正の相関(positive correration)があるといいます.これに反し,
は正の相関(positive correration)があるといいます.これに反し,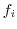 が増加するとき,
が増加するとき,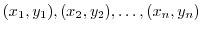 が減少する傾向があるとき,
が減少する傾向があるとき,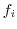 と
と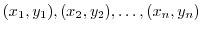 は負の相関(negative correration)があるといいます.
は負の相関(negative correration)があるといいます.
![\includegraphics[width=10cm]{STATFIG/Fig1-3-1.eps}](img88.png)
相関表
相関図ではデータの数が非常に多い場合には,その図示が困難となる場合があります.そのような場合には,2つの変量を同時に考えた度数分布表として表わすと便利です.このような表を相関表といいます.
回帰直線
二酸化硫黄と二酸化窒素の関係のように,変量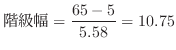 の値
の値
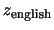 に,変量
に,変量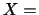 の値
の値
 がそれぞれ対応していると仮定します.このとき,平面上の
がそれぞれ対応していると仮定します.このとき,平面上の 個の点:
個の点:
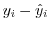
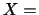 軸方向の距離が,ある意味で最も近い直線(回帰直線(linear regression)):
軸方向の距離が,ある意味で最も近い直線(回帰直線(linear regression)):
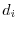
もし回帰直線が求められていれば,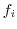 に対する
に対する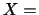 の値(予測値
の値(予測値
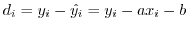 )は
)は
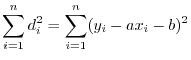
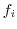 に対する実際の値(観測値)は
に対する実際の値(観測値)は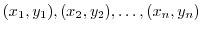 です.そこでこの2つの値の差
です.そこでこの2つの値の差
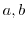 を予測誤差といい
を予測誤差といい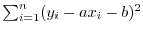 で表わします.
で表わします.
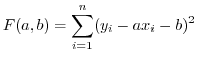
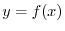
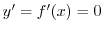 の値を定め,最適合直線を求める方法を最小2乗法(method of least square)といいます.
の値を定め,最適合直線を求める方法を最小2乗法(method of least square)といいます.
では,どうすれば
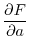 を最小にする
を最小にする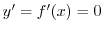 を求めることができるでしょうか.ここで,
を求めることができるでしょうか.ここで,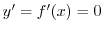 の値が変化することにより,
の値が変化することにより,
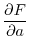 の値が変化するので,
の値が変化するので,
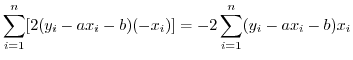
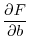 が極値をとる点では何が起きているかを思い出すと,
が極値をとる点では何が起きているかを思い出すと,
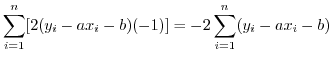 となります.このことを,
となります.このことを,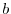 と
と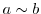 という変数に対して行うと,
という変数に対して行うと,
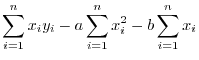 |
 |
![$\displaystyle \sum_{i=1}^{n}[2(y_{i} - ax_{i} - b)(-x_{i})] = -2\sum_{i=1}^{n}(y_{i} - ax_{i}-b)x_{i}$](img104.png) |
|
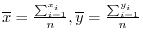 |
 |
![$\displaystyle \sum_{i=1}^{n}[2(y_{i} - ax_{i} - b)(-1)] = -2\sum_{i=1}^{n}(y_{i} - ax_{i}-b)$](img106.png) |
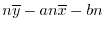 |
 |
0 | |
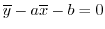 |
 |
0 |
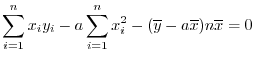 であることに注意すると,上の2式は次のように書きなおせます.
であることに注意すると,上の2式は次のように書きなおせます.
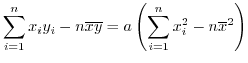 |
 |
0 | |
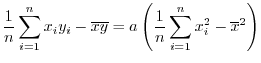 |
 |
0 |
第2式から,
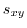 となるので,これを第1式に代入すると,
となるので,これを第1式に代入すると,
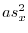
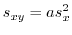
 で割ると,
で割ると,
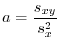
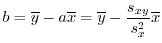 ,右辺はaかける
,右辺はaかける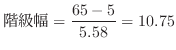 の分散
の分散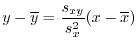 です.したがって,
です.したがって,
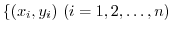
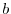 は
は
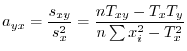
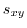 より,
より,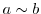 を求めると,
を求めると,
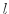
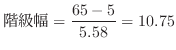 上の
上の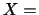 の回帰直線
の回帰直線
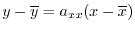
 個のデータ
個のデータ
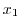 について,
について,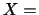 の
の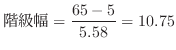 への回帰係数は
への回帰係数は
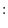
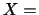 の
の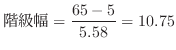 への回帰直線
への回帰直線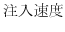 の方程式は
の方程式は
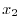
重回帰分析
回帰直線を用いることができるのはデータが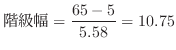 ,
,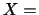 の時だけではありません.例えば,自動車の部品メーカーでは,あるセラミック部品の寸法
の時だけではありません.例えば,自動車の部品メーカーでは,あるセラミック部品の寸法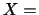 を精度よく予測する課題に取り組むことになった.
を精度よく予測する課題に取り組むことになった.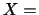 を予測するための変数として,次の3つの変数が考えられている.
を予測するための変数として,次の3つの変数が考えられている.
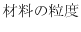 |
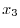 |
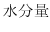 |
|
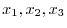 |
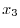 |
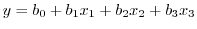 |
|
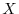 |
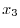 |
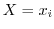 |
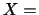 を予測するために3つの変数
を予測するために3つの変数
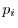 を用いることになる.このとき,
を用いることになる.このとき,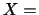 を目的変数,
を目的変数,
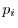 を説明変数といいます.この場合,回帰直線は
を説明変数といいます.この場合,回帰直線は
|