Next: 確率変数 Up: 確率モデル Previous: 確率の定義 目次
1. ![]() = [さいころを4回投げて少なくとも1回6の目がでる].
= [さいころを4回投げて少なくとも1回6の目がでる]. ![]() = [2個のさいころを同時に24回投げて少なくとも1回2個とも6の目がでる] とするとき,
= [2個のさいころを同時に24回投げて少なくとも1回2個とも6の目がでる] とするとき,
2. ある患者がある種の症状を訴えてきた.医師の経験から,同じ年齢層の人がその症状を訴えるとき,約5%の人がガンであることを知っている.一方,ある精密検査によって真のガン患者に対しては85%の陽性反応を示し,ガン患者でない人にも5%の陽性反応を示す.もしある患者がその精密検査の結果陽性反応を示した場合,その患者がガン患者である確率を求めよう.
3. 次の関係を示そう.
1.
(a) 4回投げて少なくとも1回6の目がでるという事象![]() の余事象
の余事象
![]() は,4回投げて一度も6の目がでないとなります.ここで,それぞれの回に6の目がでない確率は
は,4回投げて一度も6の目がでないとなります.ここで,それぞれの回に6の目がでない確率は
![]() に注意すると,
に注意すると,
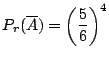
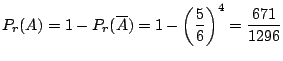
(b) 2個のさいころを同時に24回投げて少なくとも1回2個とも6の目がでるという事象![]() を考えます.まず,2個のさいころを同時に投げたとき,2個とも6の目がでる確率は
を考えます.まず,2個のさいころを同時に投げたとき,2個とも6の目がでる確率は
![]() .
.
ここで,![]() の余事象
の余事象
![]() は,2個のさいころを同時に24回投げて一度も2個両方は6の目ではないとなります.
したがって,
は,2個のさいころを同時に24回投げて一度も2個両方は6の目ではないとなります.
したがって,
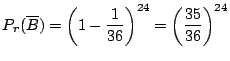
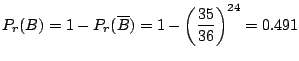
2 ![]() 「真のガン患者」,
「真のガン患者」,![]() 「精密検査で陽性反応がでた患者」とおくと質問は,患者がその精密検査の結果陽性反応を示した場合にガン患者である確率を求めることです.これは条件付き確率を用いると次のように表わせます.
「精密検査で陽性反応がでた患者」とおくと質問は,患者がその精密検査の結果陽性反応を示した場合にガン患者である確率を求めることです.これは条件付き確率を用いると次のように表わせます.
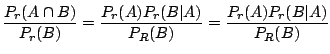 |
|||
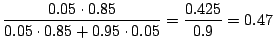 |
別解
3.