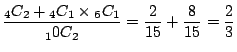Next: 確率の公理 Up: 確率モデル Previous: 確率モデル 目次
(a) まず,場合の数を使って確率を求めてみましょう.
![$X_{i} = [6回中i回1の目がでる]$](img2.png) とおきます.
とおきます.
さいころを6回投げると,目のでかたは全部で
![]() 通りあります.次に1の目が6回中1回出る場合の数は何通りあるか数えてみましょう.
通りあります.次に1の目が6回中1回出る場合の数は何通りあるか数えてみましょう.
一投目で1の目が出ると,残りの5回は1以外なので,
![]() 通り.同じことが二投目,三投目,... でも言えるので,全部で
通り.同じことが二投目,三投目,... でも言えるので,全部で
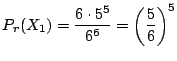
別解
まず,1の目が1回出るのは最初の1投目でも2投目でも6投目でもいいので全部で6通りあることに注意します.この6通りのそれぞれの確率を調べてみましょう.まず,1投目で1の目が出たとすると
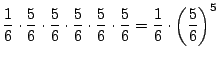
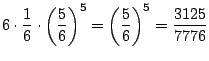
(b) 1の目が4回出る組み合わせは全部で
![]() 通り.そのとき,残りの2回は1以外なので
通り.そのとき,残りの2回は1以外なので![]() 通り.よって全部で,
通り.よって全部で,
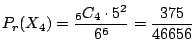
別解
6回中4回1の目がでる組み合わせは
![]() 通り.また,それぞれの確率は
通り.また,それぞれの確率は
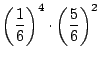
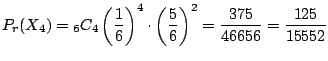
![$\displaystyle 1 - \left[\binom{6}{5} \cdot \left(\frac{1}{6}\right)^5 \left(\fr...
...) + \binom{6}{6} \cdot \left(\frac{1}{6}\right)^6 \right] = \frac{46625}{46656}$](img94.gif) |
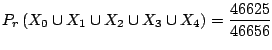
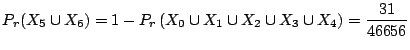
2.
(a) 白玉5個,赤玉3個,黒玉が2個合わせて10個の中から4個を取り出す組み合わせは
![]() 通り.次に白玉4個を袋の中から取り出す組み合わせを考えてみましょう.
通り.次に白玉4個を袋の中から取り出す組み合わせを考えてみましょう.
袋の中の5個の白玉から4個を取り出すしかないので,その組み合わせは
![]() 通り.したがって,取り出した4個が全て白玉の確率は
通り.したがって,取り出した4個が全て白玉の確率は
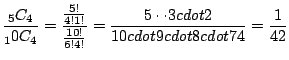
別解 取り出した4個に注目.
1. 白玉4個取り出す組み合わせは
![]() 通り
通り
2. 白玉1個ずつ取り出す確率は,
![]()
したがって,取り出した4個が全て白玉の確率は
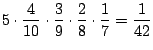
(b) 白玉5個,赤玉3個,黒玉が2個合わせて10個の中から4個を取り出す組み合わせは
![]() 通り.次に白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
通り.次に白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
2個だけ白玉ということは5個の白玉から2個取り出し,残りの赤玉と黒玉から2個取り出す場合の数なので,
![]() .したがって,取り出した4個のうち白がちょうど2個である確率は
.したがって,取り出した4個のうち白がちょうど2個である確率は
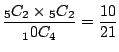
(c) 白が2個以内とは白が0個,1個,2個の事象の場合である.よって,その確率は
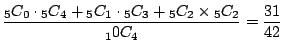
(d) 白が2個赤が2個を取り出す組み合わせは,
![]() である.したがって,取り出した4個のうち白が2個赤が2個である確率は
である.したがって,取り出した4個のうち白が2個赤が2個である確率は
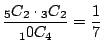
1. 白,赤,黒がともに含まれるということは,白,赤,黒のどれかが2個になる組み合わせを考えればよい.よって
![]() 通り.
通り.
2. 白,赤,黒1つずつ取り出す確率は
![]() .
.
3.したがって,白,赤,黒がともに含まれる確率は
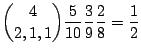
3.
(a) 1から10までがその順に一列に並ぶ場合を考えているので,まずは,1から10を勝手に一列に並べる並べ方は何通りあるか考えてみましょう.
先頭にくるのは1から10の内どれでもよいので,10通り,次は9通り,...となるので,全部で
![]() 通りとなります.
通りとなります.
次に1から10までがその順に一列に並ぶ場合は一通り.したがって,その確率は
別解 1が先頭にくる確率は
![]() ,1が先頭にきたことが分ったあと,2が2番目にくる確率は
,1が先頭にきたことが分ったあと,2が2番目にくる確率は
![]() ,1が先頭,2が2番目にきたことが分ったあと,3が3番目にくる確率は
,1が先頭,2が2番目にきたことが分ったあと,3が3番目にくる確率は
![]() ,...となるので,1から10までがその順に一列に並ぶ確率は
,...となるので,1から10までがその順に一列に並ぶ確率は
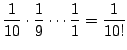
(b) 4のカードがちょうど4番目ということは,それ以外の9枚のカードはどこにあってもいいので,4のカードがちょうど4番目にくるのは
![]() 通りあります.よってその確率は
通りあります.よってその確率は
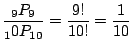
別解 4のカードがちょうど4番目にくる確率は
![]()
(c) 1が最初に,4が4番目にあるということは,それ以外の8枚のカードはどこにあってもいいので,全部で
![]() 通り.よって,1が最初に,4が4番目にくる確率は
通り.よって,1が最初に,4が4番目にくる確率は
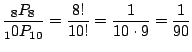
別解 1が最初にくる確率は
![]() .次に1が最初にきたことが分ったあと,4が4番目にくる確率は
.次に1が最初にきたことが分ったあと,4が4番目にくる確率は
![]() .よって,1が最初に,4が4番目にくる確率は
.よって,1が最初に,4が4番目にくる確率は
4. (a) 円板の半径は1.5cmよりちょうど正方形の中に入るには,円板の中心が1辺5cmの正方形の中にあればよい.したがって,その確率は
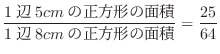
(b) A = 「円板が正方形の辺にかかる」の余事象は![]() = 「円板が正方形の中にある」となる.したがって,その確率は
= 「円板が正方形の中にある」となる.したがって,その確率は

(c) 円板が4つの正方形にまたがるには,その中心が4つの正方形の境界から1.5cm以内になければならない.また,その面積は
![]() .したがって,円板が4つの正方形にまたがる確率は
.したがって,円板が4つの正方形にまたがる確率は
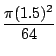
5.
(a) 白玉4個,赤玉6個,合わせて10個の中から2個を取り出す組み合わせは
![]() 通り.白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
通り.白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
袋の中の4個の白玉から2個を取り出すしかないので,その組み合わせは
![]() 通り.したがって,取り出した2個が両方白玉の確率は
通り.したがって,取り出した2個が両方白玉の確率は
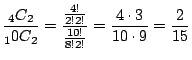
(b) 1個だけ白玉ということは4個の白玉から1個取り出し,6個の赤玉から1個取り出す場合の数なので,
![]() .よってその確率は
.よってその確率は
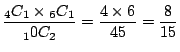
(c) 少なくとも1個は白玉という事象は,2個とも白玉であるか,または1個だけ白玉であるかのどちらかです.ここで,これらの事象は排反事象(同時に起きない)であることに注意すると,全部で,
![]() 通り.したがって,求める確率は
通り.したがって,求める確率は