Next: 標本分布 Up: 理論分布 Previous: 幾何分布 目次
1. あるガスステイションで1週間に売れるガソリンの量![]() キロリットルは,次の密度関数をもつ分布に従っているとする.
キロリットルは,次の密度関数をもつ分布に従っているとする.
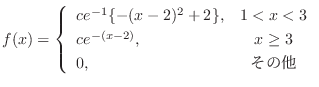
2. 日本人の血液型はA型 35%,B型 25%,AB型 10%,O型 30%であるといわれている.いま,4人いたとき,4人とも血液型が異なる確率を求めよ.
3.. 電話での通話時間は平均2分の指数分布に従うとする.電話ボックスにすでに話し中の人も含めて3人いたとき,10分以上待たなければならない確率を求めよ.
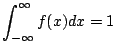
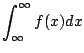 |
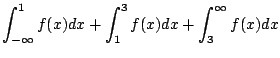 |
||
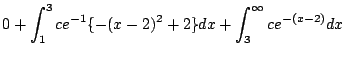 |
|||
![$\displaystyle ce^{-1}\left[-\frac{1}{3}(x-2)^{3} + 2x \right]_{1}^{3} - \left[ce^{-(x-2)}\right]_{3}^{\infty}$](img646.gif) |
|||
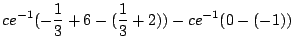 |
|||
2. ![]() をA型の人の数,
をA型の人の数,![]() をB型の人の数,
をB型の人の数,![]() をAB型の人の数,
をAB型の人の数,![]() をO型の人の数とすると,
をO型の人の数とすると,
![]() .よって
.よって
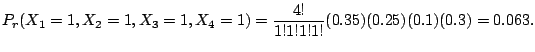
3.
![]() を3人の通話時間とおくと,
を3人の通話時間とおくと,
![]() .ここで
.ここで
![]() とおくと
とおくと![]() は3人の通話時間の合計を表わす.言い換えると待ち時間を表わし,
は3人の通話時間の合計を表わす.言い換えると待ち時間を表わし,
![]() .また
.また
![]() より
より
![]() .よって10分以上待たなければならない確率は
.よって10分以上待たなければならない確率は
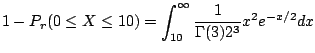 |
|||
![$\displaystyle 1 - \frac{1}{16}\int_{0}^{10}x^2 e^{-x/2}dx = 1 - [-2x^2 e^{-x/2}\mid_{0}^{10} + 4\int_{0}^{10}xe^{-x/2}dx ]$](img661.gif) |
|||
![$\displaystyle 1 - \frac{1}{16}[-200e^{-5} + 4(-2xe^{-x/2}\mid_{0}^{10} + 2\int_{0}^{10}e^{-x/2}dx)]$](img662.gif) |
|||
![$\displaystyle 1 - \frac{1}{16}[-200e^{-5} -80e^{-5} - 16e^{-x/2}\mid_{0}^{10}] = 1 - \frac{1}{16}[-296e^{-5} + 16] = \frac{296 e^{-5}}{16} = 0.1246$](img663.gif) |