next up previous contents
Next: ポワソン分布 Up: 理論分布 Previous: 理論分布   目次

2項分布

数理統計演習問題 8

1. 2項分布 $ B(8,0.4), B(8,0.2)$の確率分布を求めよ．

2. プラモデルが25セットあり，そのうち2セットは部品がかけているとする．客が任意に3セット選ぶとき，いずれも完全なセットである確率を求めよ．

3. ある試薬をネズミに注射すると一定期間のうちに$ 40\%$が死亡するという．8匹のネズミにその試薬を注射した場合，

(a)
8匹全部が一定期間以上生存する確率を求めよ．
(b)
$ 95\%$の確率で，8匹のうち何匹以上が生存するということができるか．

問題解答

1. $ p_{r} = P(X = r) = \binom{8}{r}(0.4)^{r}(0.6)^{1-r}$より

\begin{displaymath}\begin{array}{\vert c\vert c\vert c\vert c\vert c\vert c\vert... ....2322 & 0.1239 & 0.0413 & 0.0079 & 0.0007 \hline \end{array}\end{displaymath}

$ p_{r} = P(X = r) = \binom{8}{r}(0.2)^{r}(0.8)^{1-r}$より

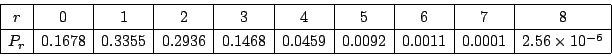
\begin{displaymath}\begin{array}{\vert c\vert c\vert c\vert c\vert c\vert c\vert... ...2 & 0.0011 & 0.0001 & 2.56 \times 10^{-6} \hline \end{array}\end{displaymath}

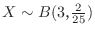2. プラモデルを取り出す試行はベルヌーイ試行． $ X$を部品がかけているプラモデルのセットの数とすると， $X \sim B(3，\frac{2}{25})$．よって，選んだ３セットが全て完全なセットである確率は

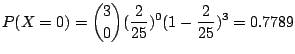
$\displaystyle P(X = 0) = \binom{3}{0}(\frac{2}{25})^{0}(1 - \frac{2}{25})^{3} = 0.7789$

3. $ X$を注射のあと一定期間生存できずに死亡するねずみの数とすると， $ X \sim B(8,0.4)$となり，Iで求めた確率分布が使える．

(a) ８匹全部が一定期間生存する確率は

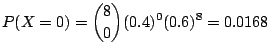
$\displaystyle P(X = 0) = \binom{8}{0}(0.4)^{0}(0.6)^{8} = 0.0168$

(b) $ r$を95%以上の確率で生存できないねずみの数となるとすると，$ X$の分布関数$ F(x)$は

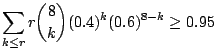$\displaystyle F(r) = P(X \leq r)$ $\displaystyle =$ $\displaystyle \sum_{k \leq r} r\binom{8}{k}(0.4)^{k}(0.6)^{8-k} \geq 0.95$  

を満たす．ここで，Iの確率分布を用いると $ P(X = 0) = 0.168, P(X=1) = 0.0896$より，$ r = 1$となり，$ 95\%$で生存できるねずみの数は７匹以上となる．