Next: 確率モデル Up: 個数の処理 Previous: 個数の処理 目次
番号のついた 個の異なったものをある規則のもとに順に並べたものを順列(permutation)といい,順列の総数を順列の数という.
個の異なったものをある規則のもとに順に並べたものを順列(permutation)といい,順列の総数を順列の数という.
 個のものから
個のものから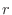 個とって1列に並べる順列の数は
個とって1列に並べる順列の数は
|
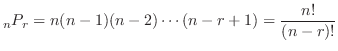
|
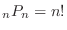 ,
,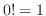 とする.
とする.
 個のものから重複を許して
個のものから重複を許して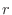 個とる順列の数は
個とる順列の数は
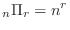
 個のものを円形に並べる順列の数は
個のものを円形に並べる順列の数は
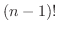
 個のもののうち,
個のもののうち,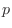 個,
個,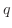 個,
個, 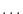 ,
, 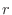 個がそれぞれ同じであるとき,これらを1列に並べる順列の数は
個がそれぞれ同じであるとき,これらを1列に並べる順列の数は
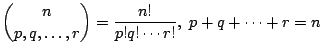
並べる順序は考えずに,複数個から幾つか選んだ組を組合せ(combination)という.
 個のものから
個のものから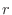 個とる組み合わせの数は
個とる組み合わせの数は
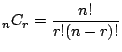
である.特に,
![]() ,
,
![]() とする.
とする.
 個の物を,
個の物を,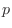 個,
個,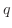 個,
個, 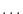 ,
, 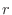 個の組に分ける組合せの数は
個の組に分ける組合せの数は
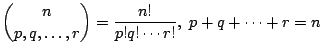
 個の異なるものから,繰り返しを許して,
個の異なるものから,繰り返しを許して,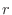 個とるときの組合せの数は
個とるときの組合せの数は
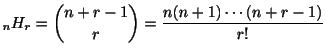
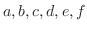 の文字を一列に並べるのに次の場合は何通りあるか求めよう.
の文字を一列に並べるのに次の場合は何通りあるか求めよう.
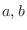 が隣あう場合
が隣あう場合
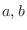 が隣合わない場合
が隣合わない場合
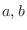 が両端にくる場合
が両端にくる場合
5.
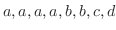 の8個の文字を並べる順列の総数は
の8個の文字を並べる順列の総数は
![]() で与えられることを示せ.
で与えられることを示せ.