Next: F分布(F distribution) Up: 標本分布 Previous: 分布(Chi square distribution) 目次
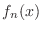 が
が
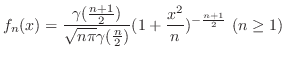
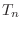 を自由度
を自由度 の
の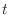 分布という。
分布という。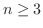 のとき,その期待値と分散は
のとき,その期待値と分散は
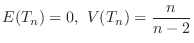
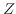 を標準正規確率変数,
を標準正規確率変数,
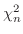 を自由度
を自由度 の
の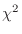 確率変数とする。さらに,
確率変数とする。さらに,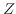 と
と
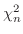 が互いに独立ならば,標本分布
が互いに独立ならば,標本分布
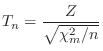
 の
の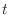 分布に従う。
分布に従う。
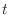 分布の正規近似
分布の正規近似
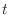 分布は自由度が大きければ標準正規分布で近似でき,
分布は自由度が大きければ標準正規分布で近似でき,
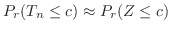
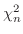 は
は 個の独立な確率変数の和であるから,
個の独立な確率変数の和であるから, が大きければ
が大きければ
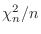 は大数の法則により,1に収束する。
は大数の法則により,1に収束する。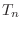 確率変数の分母が1に近づくから,
確率変数の分母が1に近づくから,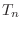 確率変数は分子の標準正規確率変数と変わらなくなる。
確率変数は分子の標準正規確率変数と変わらなくなる。