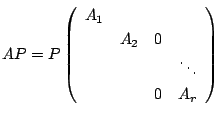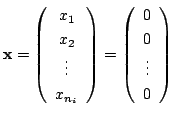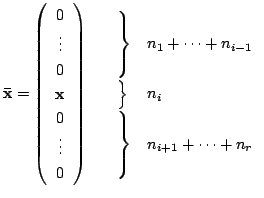: Jordan標準形
: Jordan標準形
: Jordan標準形
目次
索引
 広義固有空間
広義固有空間

 を
を 次正方行列とし,
次正方行列とし,  を
を
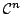 の部分空間とします.
の部分空間とします. に属する任意のベクトル
に属する任意のベクトル
 に対して
に対して
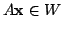 となるとき, 部分空間
となるとき, 部分空間 はA - 不変(A - invariant)であるといいます.
はA - 不変(A - invariant)であるといいます.
行列 の固有多項式を固有値の重複度でまとめて
の固有多項式を固有値の重複度でまとめて
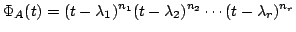 |
(5.1) |
と表します.ここで, 固有値
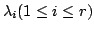 に対して
とおくと包含関係
が成り立つ.次元を考えれば, これは無限には続かず
となります.このとき
に対して
とおくと包含関係
が成り立つ.次元を考えれば, これは無限には続かず
となります.このとき
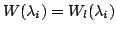 です.
です.
|
|
証明
(1) 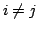 のとき,
のとき,
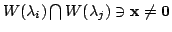 となるベクトル
となるベクトル
 が存在したとする.このとき
が存在したとする.このとき
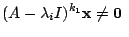
かつ
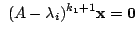
を満たす0以上の整数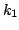 がある.
がある.
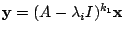 とおくと
となる.
とおくと
となる.
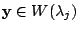 より,
より,
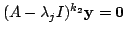 となる整数
となる整数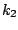 がある.しかし,
がある.しかし,
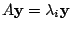 より
より
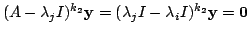 となるが,
となるが, 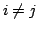 のとき
のとき
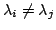 としたので, これは矛盾である.
としたので, これは矛盾である.
(2)
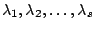 を
を の相異なる固有値とする.
の相異なる固有値とする.
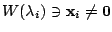
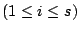 に対して
に対して
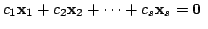
ならば
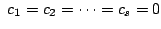
が成り立つことを帰納法を用いて示す.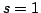 の場合は明らかなので
の場合は明らかなので
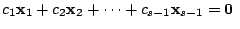
のとき
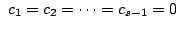
が成り立つと仮定する.条件より
が成り立つので,
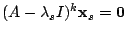 となる整数
となる整数 をとり, 上の式(**)の両辺に左からかけると
をとり, 上の式(**)の両辺に左からかけると
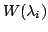 は
は
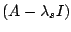 - 不変より,
- 不変より,
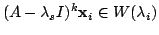 となる.また, (1)より
となる.また, (1)より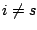 のとき
のとき
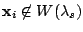 .したがって,
.したがって,
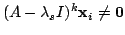
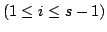 となる.これより帰納法の仮定が使えて,
となる.これより帰納法の仮定が使えて,
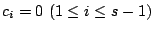 を得る.よって,
を得る.よって,
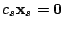 となり,
となり, 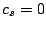 を得る.
を得る.
(3) (2)で示した1次独立性より
が成り立つ.また,
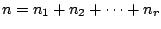 なので, (3)を示すには
なので, (3)を示すには

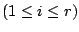 をいえばよい.
をいえばよい.
行列 は, 定理4.3より, ユニタリ行列
は, 定理4.3より, ユニタリ行列 を用いて次の形に三角化できる.
を用いて次の形に三角化できる.
いま,
とおくと, 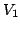 は
は
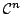 の
の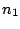 次元部分空間になる.また,
次元部分空間になる.また,
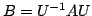 の形より
の形より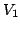 の任意のベクトル
の任意のベクトル
 に対して
が成り立つ.ここで,
に対して
が成り立つ.ここで,  は正則なので
となる.したがって,
は正則なので
となる.したがって,
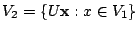 とおくと,
とおくと, 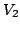 は
は
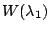 に含まれる
に含まれる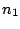 次元の部分空間になり, 不等式
次元の部分空間になり, 不等式
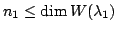 を得る.固有値の順番を入れ替えて考えれば,
を得る.固有値の順番を入れ替えて考えれば,

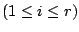 が成り立つ.
が成り立つ.

|
|
証明
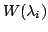 から基底
から基底
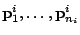 をとる.
をとる.
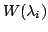 は
は - 不変なので,
- 不変なので,
と表せる.ここで
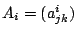 とおくと,
とおくと, 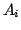 は
は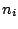 次正方行列である.定理5.1より
は
次正方行列である.定理5.1より
は
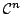 の基底となる.したがって,
とおくと,
の基底となる.したがって,
とおくと,  は正則行列となり
を満たす.この式の両辺に
は正則行列となり
を満たす.この式の両辺に を左からかければ求める式を得る.
を左からかければ求める式を得る.
この関係式を用いると
となる.したがって, 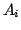 の固有値が
の固有値が
 だけであることを示せば
が示される.
だけであることを示せば
が示される.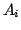 が
が
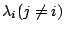 を固有値として持ち,
を固有値として持ち,
 に対する固有ベクトル
が取れたとする.すなわち,
に対する固有ベクトル
が取れたとする.すなわち,
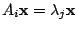 とする.このとき
とおくと,
とする.このとき
とおくと,
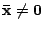 で
で
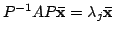 を満たす.したがって,
は
を満たす.したがって,
は
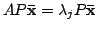 , つまり,
, つまり,
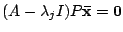 を満たす.しかし, これは
を満たす.しかし, これは
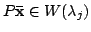 を意味し, 定理5.1に矛盾する.
を意味し, 定理5.1に矛盾する.






: Jordan標準形
: Jordan標準形
: Jordan標準形
目次
索引
yokotalab
平成20年3月7日
![]() 広義固有空間
広義固有空間
![]()
![]() を
を![]() 次正方行列とし,
次正方行列とし, ![]() を
を
![]() の部分空間とします.
の部分空間とします.![]() に属する任意のベクトル
に属する任意のベクトル
![]() に対して
に対して
![]() となるとき, 部分空間
となるとき, 部分空間![]() はA - 不変(A - invariant)であるといいます.
はA - 不変(A - invariant)であるといいます.
![]() の固有多項式を固有値の重複度でまとめて
の固有多項式を固有値の重複度でまとめて
![]() のとき,
のとき,
![]() となるベクトル
となるベクトル
![]() が存在したとする.このとき
が存在したとする.このとき
![]() を
を![]() の相異なる固有値とする.
の相異なる固有値とする.
![]()
![]() に対して
に対して
![]() は, 定理4.3より, ユニタリ行列
は, 定理4.3より, ユニタリ行列![]() を用いて次の形に三角化できる.
を用いて次の形に三角化できる.

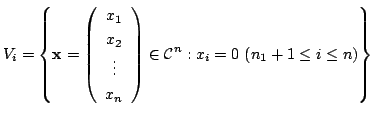
![]() から基底
から基底
![]() をとる.
をとる.
![]() は
は![]() - 不変なので,
- 不変なので,