Next: レイアウト Up: 数値積分法 Previous: Simpsonによる数値積分 目次 索引

シンプソン法は、図![[*]](crossref.png) において、関数
において、関数![]() を
を
![]() まで積分するのに,3点
まで積分するのに,3点
![]() を通る2次関数で近似する方法で、台形公式による方法より精度の高い近似値が得られる。
下図のように、3点
を通る2次関数で近似する方法で、台形公式による方法より精度の高い近似値が得られる。
下図のように、3点
![]() を通る2次関数と
を通る2次関数と![]() 軸の区間
軸の区間![]() ではさまれた網掛け部分の面積
ではさまれた網掛け部分の面積![]() は、
は、
2次関数を
![]() とおくと
とおくと
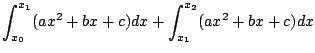 |
|||
![$\displaystyle \left[\frac{ax^{3}}{3} + \frac{bx^{2}}{2} + cx\right]_{x_0}^{x_1} + \left[\frac{ax^{3}}{3} + \frac{bx^{2}}{2} + cx\right]_{x_1}^{x_2}$](img131.gif) |
|||
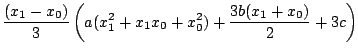 |
|||
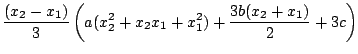 |
|||
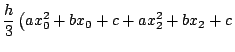 |
|||
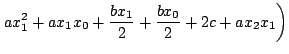 |
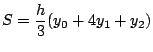
図![[*]](crossref.png) のように関数
のように関数![]() が区間
が区間![]() で
で![]() (偶数)等分されていると,この区間の面積の近似値
(偶数)等分されていると,この区間の面積の近似値![]() は
は
![$\displaystyle \frac{h}{3}\left[(y_{0} + 4y_{1} + y_{2}) + (y_{2} + 4y_{3} + y_{4}) + \cdots + (y_{n-2} + 4y_{n-1} + y_{n})\right]$](img142.gif) |
|||
![$\displaystyle \frac{h}{3}\left[y_{0} + y_{n} + 2\sum_{i=1}^{(n/2)-1}y_{2i} + 4\sum_{i=1}^{n/2}y_{2i-1}\right]$](img143.gif) |
