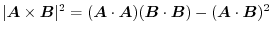Next: Directional cosine Up: Vector Previous: Inner product Contents Index
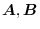 , the size is the area of ?the parallelogram created by
, the size is the area of ?the parallelogram created by
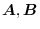
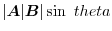 , the direction is perpendicular to both
, the direction is perpendicular to both
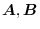 , and
, and
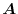 is rotating within
is rotating within
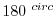 and overlapping in the direction of
and overlapping in the direction of
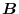 , the vector determined as the direction of the right-handed screw is the cross product of
, the vector determined as the direction of the right-handed screw is the cross product of
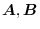 ( cross product) is called
( cross product) is called
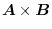 .For
.For
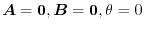 .
.
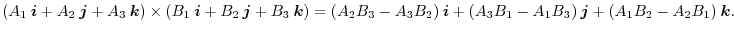
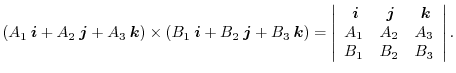
![$\boldsymbol{A} = {}^t[1\ 2\ 1], \boldsymbol{B} = {}^t[2\ -1\ -2]$](img42.png) ,find
,find
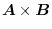 .
.
Answer
![$\left\vert\begin{array}{rrr}
\:\boldsymbol{i} & \:\boldsymbol{j} & \:\boldsymbo...
...= -3\:\boldsymbol{i} + 4\:\boldsymbol{j} + -5\:\boldsymbol{k} = {}^t[-3\ 4\ -5]$](img43.png)
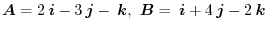 ,find the following vectors:.
(1)
,find the following vectors:.
(1)
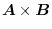
(2)
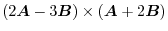
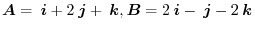 .
.
(1) Find the area of the parallelogram when these are regarded as two adjacent sides. (2) Find a vector other than the zero vector that is orthogonal to these.